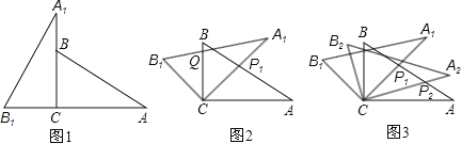
【题目】将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图2中,若AP1=a,则CQ等于多少?
(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?
参考答案:
【答案】(1)证明见解析;(2)CQ=![]() a;(3)当∠P1CP2=∠P1AC=30°时, P1P2=
a;(3)当∠P1CP2=∠P1AC=30°时, P1P2=![]() CP1
CP1
【解析】试题分析:(1)根据△A1B1C和△ABC是两个完全一样的三角形,顺时针旋转45°两个条件证明△B1CQ≌△BCP1,然后可求证:CP1=CQ;
(2)作P1D⊥AC于D,根据∠A=30,∠P1CD=45°分别求出P1D=![]() AP1,CP1=
AP1,CP1=![]() P1D=
P1D=![]() AP1,而AP1=a可求CQ.
AP1,而AP1=a可求CQ.
(3)当△A P1C∽△CP1P2时,∠P1CP2=∠P1AC=30°,再根据相似求出CP1与P1P2之间存在的数量关系;
试题解析:
(1)∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°;
又B1C=BC,∠B1=∠B,
∴△B1CQ≌△BCP1(ASA)
∴CQ=CP1;
(2)如图:作P1D⊥AC于D,
∵∠A=30°,
∴P1D=![]() AP1;
AP1;
∵∠P1CD=45°,
∴![]() =sin45°=
=sin45°=![]() ,
,
∴CP1=![]() P1D=
P1D=![]() AP1;
AP1;
又AP1=a,CQ=CP1,
∴CQ=![]() a;
a;
(3)当∠P1CP2=∠P1AC=30°时,由于∠CP1P2=∠AP1C,则△AP1C∽△CP1P2,
所以将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C时,有△AP1C∽△CP1P2.
这时![]() =
=![]() =
=![]() ,
,
∴P1P2=![]() CP1.
CP1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:
(1)甲、乙两名学生在同一餐厅用餐的概率;
(2)甲、乙两名学生至少有一人在B餐厅的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业决定用
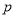 万元援助灾区
万元援助灾区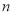 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第 所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中
所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中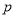 ,
,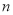 ,
,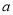 都是正整数)
都是正整数)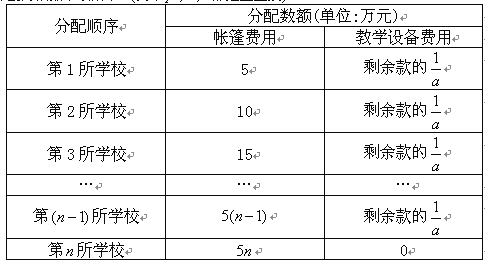
根据以上信息,解答下列问题:
(1)写出
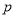 与
与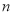 的关系式;
的关系式;(2)当
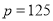 时,该企业能援助多少所学校?
时,该企业能援助多少所学校?(3)根据震区灾情,该企业计划再次提供不超过
 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若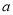 由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
由 (2)确定,则再次提供的捐款最多又可以援助多少所学校? -
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:
(1)-2018-20182+20192;(2)1252-50×125+252.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
 BC,连结CD和EF.
BC,连结CD和EF.
(Ⅰ)求证:四边形CDEF是平行四边形;
(Ⅱ)求四边形BDEF的周长.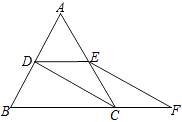
-
科目: 来源: 题型:
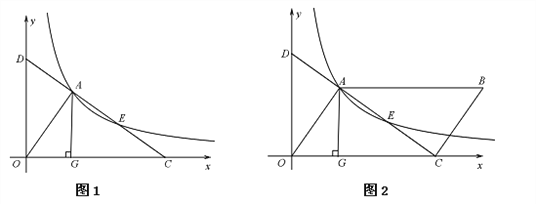
查看答案和解析>>【题目】如图1,直线
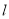 交x轴于点C,交y轴于点D,与反比例函数
交x轴于点C,交y轴于点D,与反比例函数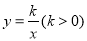 的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.
的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.(1)k = ;
(2)求证:AD =CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积
相关试题

