搜索
【题目】家乐福超市“端午节”举行有奖促销活动：凡一次性购物满200元者即可获得一次摇奖机会.摇奖机是一个圆形转盘，被分成16等分，摇中红、黄、蓝色区域，分获一、二、三等奖，奖金依次为48元、40元、32元.一次性购物满200元者，如果不摇奖可返还现金15元.
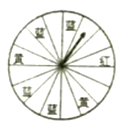
（1）摇奖一次，获一等奖的概率是多少？
（2）小明一次性购物满了200元，他是参与摇奖划算还是领15元现金划算，请你帮他算算.
参考答案：
【答案】(1) 
；(2) 转转盘划算.
【解析】
（1）找到红色区域的份数占总份数的多少即为获得一等奖的概率，
（2）游戏是否合算，关键要看游戏双方获胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
解：（1）整个圆周被分成了16份，红色为1份，
∴获得一等奖的概率为：，
（2）转转盘：
元，
∵16元>15元，
∴转转盘划算.
-
科目： 来源： 题型：
查看答案和解析>>【题目】星期天，玲玲骑自行车到郊外游玩，她离家的距离与时间的关系如图所示，请根据图象回答下列问题．
（1）玲玲到达离家最远的地方是什么时间？离家多远？
（2）她何时开始第一次休息？休息了多长时间？
（3）她骑车速度最快是在什么时候？车速多少？
（4）玲玲全程骑车的平均速度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D，点F为OE的延长线上一点且OC2=OD·OF.
（1）求证：CF为⊙O的切线.
（2）已知DE=2，
.①求⊙O的半径；②求sin∠BAD的值
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A，且点A的横坐标为4．（1）求点A的坐标及一次函数的解析式；
（2）若直线x=2与反比例函数和一次函数的图象分别交于点B、C，求线段BC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线y=ax2﹣5ax+4a与x轴交于A、B（A点在B点的左侧）与y轴交于点C．
（1）如图1，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；
（2）如图2，点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的横坐标；
（3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=﹣4
a，连接KB并延长交抛物线于点Q，求PQ的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索归纳：
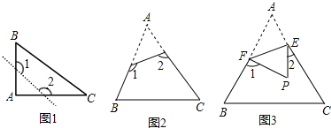
（1）如图1，已知△ABC为直角三角形，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2等于______；
（2）如图2，已知△ABC中，∠A=40°，剪去∠A后成四边形，则∠1+∠2=______；
（3）如图2，根据（1）与（2）的求解过程，请你归纳猜想∠1+∠2与∠A的关系是______；
（4）如图3，若没有剪掉，而是把它折成如图3形状，试探究∠1+∠2与∠A的关系并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，D是等边△ABC的边BA上一动点（点D与点B不重合），连接DC，以DC为边，在BC上方作等边△DCF，连接AF，你能发现AF与BD之间的数量关系吗？并证明你发现的结论；
（2）如图②，当动点D运动至等边△ABC边BA的延长线时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？若成立，请证明；
（3）Ⅰ.如图③，当动点D在等边△ABC边BA上运动时（点D与B不重合），连接DC，以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你的探究的结论；
Ⅱ．如图④，当动点D在等边△ABC的边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．
相关试题
