【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
参考答案:
【答案】(1)玲玲到离家最远的地方需要12时,此时离家30千米;(2)10点半时开始第一次休息;休息了半小时;(3)玲玲在返回的途中最快,速度为:15千米/时;(4)10千米/时.
【解析】
(1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;
(2)休息是路程不再随时间的增加而增加;
(3)往返全程中回来时候速度最快,用距离除以所用时间即可;
(4)用玲玲全称所行的路程除以所用的时间即可.
观察图象可知:(1)玲玲到达离家最远的地方是在12时,此时离家30千米;
(2)10点半时开始第一次休息;休息了半小时;
(3)在返回的途中,速度最快,速度为:30÷(15﹣13)=15千米/时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的AC边在直线m上,∠ACB=80°,以C为圆心,
 BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心,
BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心,  D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心,
D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心,  D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= .
D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= . 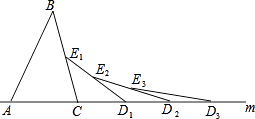
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.
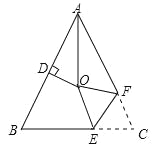
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(3,﹣3),点B的坐标为(﹣1,3),回答下列问题
(1)点C的坐标是 .
(2)点B关于原点的对称点的坐标是 .
(3)△ABC的面积为 .
(4)画出△ABC关于x轴对称的△A′B′C′.
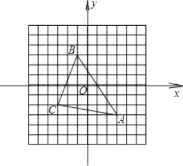
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣2012|+(3.14﹣π)0+sin30°﹣2﹣1
(2)先化简,再求值: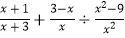 ,其中
,其中 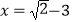 .
. -
科目: 来源: 题型:
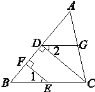
查看答案和解析>>【题目】如图所示,在△ABC中,E,G分别是BC,AC上的点,D,F是AB上的点,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2, 试判断∠AGD和∠ACB是否相等,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格图中小方格都是边长为1个单位长度的小正方形,已知三角形ABC的三个顶点都在网格的格点上,按要求完成下列各小题.
(1)请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;
(2)在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.
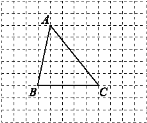
相关试题

