Question

【题目】探索归纳：

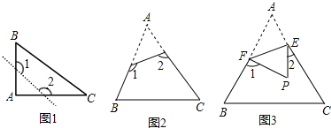
（1）如图1，已知△ABC为直角三角形，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2等于______；

（2）如图2，已知△ABC中，∠A=40°，剪去∠A后成四边形，则∠1+∠2=______；

（3）如图2，根据（1）与（2）的求解过程，请你归纳猜想∠1+∠2与∠A的关系是______；

（4）如图3，若没有剪掉，而是把它折成如图3形状，试探究∠1+∠2与∠A的关系并说明理由．

Answer 1

【答案】（1）270°；（2）220°；（3）∠1+∠2=180°+∠A ；（4）∠1+∠2=2∠A，理由见解析

【解析】

（1）先求出∠B+∠C的度数，再根据四边形内角和等于360°，即可求解；

（2）先求出∠B+∠C的度数，再根据四边形内角和等于360°，即可求解；

（3）先用∠A表示出∠B+∠C，再根据四边形内角和等于360°，即可得到结论；

（4）由折叠的性质得∠AFE=∠PFE，∠AEF=∠PEF，结合平角的定义和三角形内角和定理，即可得到结论．

（1）∵△ABC为直角三角形，∠A=90°，

∴∠B+∠C=180°-90°=90°，

∴∠1+∠2=360°-（∠B+∠C）=270°．

故答案是：270°；

（2）∵△ABC中，∠A=40°，

∴∠B+∠C=180°-40°=140°，

∴∠1+∠2=360°-（∠B+∠C）=220°．

故答案是：220°；

（3）猜想：∠1+∠2=180°+∠A，理由如下：

∵△ABC中，∠B+∠C=180°-∠A，

∴∠1+∠2=360°-（∠B+∠C）=360°-（180°-∠A）=180°+∠A．

故答案是：∠1+∠2=180°+∠A；

（4）∠1+∠2=2∠A，理由如下：

∵△EFP是由△EFA折叠得到的，

∴∠AFE=∠PFE，∠AEF=∠PEF，

∴∠1=180°-2∠AFE，∠2=180°-2∠AEF，

∴∠1+∠2=360°-2（∠AFE+∠AEF），

又∵∠AFE+∠AEF=180°-∠A，

∴∠1+∠2=360°-2（180°-∠A）=2∠A．