【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]() 是等腰三角形且BA=BF,理由见解析.
是等腰三角形且BA=BF,理由见解析.
【解析】
(1)先根据三角形的内角和得∠C=70°,由等腰三角形的性质得∠BDC=70°,从而得∠CBD的度数,可得结论;
(2)设∠BDC=∠C=α,根据三角形的内角和与三角形外角的性质分别表示∠ABD和∠DBC,相加可得结论;
(3)作垂线BT,根据角平分线的性质得:BE=BT,证明Rt△ABE≌Rt△ABT(HL),得AE=AT,证明BE是AF的垂直平分线,可得结论.
(1)如图2,△ABC中,∠A=n°=45°,∠ABC=65°,
∴∠C=180°-45°-65°=70°,
∵BD=BC,
∴∠BDC=∠C=70°,
∴∠DBC=180°-2×70°=40°,
∴∠ABD=65°-40°=25°;
(2)如图3,∠D'BC=180°-2n°,理由是:
设∠BDC=∠C=α,
∴∠DBC=180°-2α,
△ADB中,∠BDC=∠DAB+∠ABD,
即α=n°+∠ABD,
∴∠ABD=α-n°,
由翻折得:∠ABD'=∠ABD=α-n°,
∴∠D'BC=∠D'BD+∠DBC=2∠ABD+∠DBC=2(α-n°)+(180°-2α)=180°-2n°;
(3)△ABF是等腰三角形,且BF=AB,理由是:
如图4,过B作BT⊥AC于T,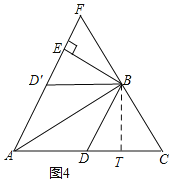
由折叠得:∠D'BA=∠DAB,
∵BE⊥AF,
∴BE=BT,
在Rt△ABE和Rt△ABT中,
∵![]() ,
,
∴Rt△ABE≌Rt△ABT(HL),
∴AE=AT,
∵AD=AD',
∴DT=D'E=TC,
∴![]() (AD+AC)=AT,
(AD+AC)=AT,
∵EF=![]() (AD+AC),
(AD+AC),
∴AT=EF=AE,
∵BE⊥AF,即BE是AF的垂直平分线,
∴BF=AB,
∴△ABF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )

A. 120°B. 135°C. 145°D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使点P到OA,OB的距离都等于a,作法如下:
①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与NM交于点P;④点P即为所求.其中③的依据是( )

A. 平行线之间的距离处处相等 B. 角的内部到角的两边的距离相等的点在角的平分线上
C. 角的平分线上的点到角的两边的距离相等 D. 线段垂直平分线上的点到线段两端点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//DG, AD∥EF,
(1)试说明:
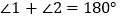 ;
;(2) 若DG是∠ADC的平分线,
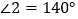 ,求∠B的度数.
,求∠B的度数.
相关试题

