【题目】已知二次函数y=kx2+2(k﹣3)x+(k﹣3)的图象开口向上,且k为整数,且该抛物线与x轴有两个交点(a,0)和(b,0).一次函数y1=(k﹣2)x+m与反比例函数y2= ![]() 的图象都经过(a,b).
的图象都经过(a,b).
(1)求k的值;
(2)求一次函数和反比例函数的解析式,并直接写出y1>y2时,x的取值范围.
参考答案:
【答案】
(1)解:由题意得,抛物线与x轴有两个交点,
令y=0,即kx2+2(k﹣3)x+(k﹣3)=0,
则△=4(k﹣3)2﹣4k(k﹣3)>0,
解得,k<3,
∵二次函数的图象开口向上,故k>0,
又∵k为整数,k﹣2≠0,
∴k=1;
(2)解:由(1)得,y=x2﹣4x﹣2,
令x2﹣4x﹣2=0得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴a+b=4,ab=﹣2,
把(a,b)代入y1=﹣x+m, ![]() 得,m=a+b=4,n=ab=﹣2
得,m=a+b=4,n=ab=﹣2
∴一次函数的表达式为y1=﹣x+4,
∴反比例函数的表达式为y2=﹣ ![]() ,
,
当y1>y2时,x<2﹣ ![]() 或0<x<2+
或0<x<2+ ![]()
【解析】(1)由抛物线与x轴有两个交点得出△=4(k﹣3)2﹣4k(k﹣3)>0,解得,k<3,又二次函数的图象开口向上,故k>0,又k为整数,k﹣2≠0,从而得出K=1 ;
(2)首先利用抛物线与x轴的交点得出其交点的横坐标,进而求出a+b=4,ab=﹣2,然后求出m,n的值,从而得出一次函数及反比例函数的解析式,画出草图,根据图像要当y1>y2时,自变量的值,主要能清楚谁大谁小,谁大就写谁的图像在上方时的自变量的取值即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55分钟;加工4个甲种零件和9个乙种零件共需85分钟,求李师傅加工2个甲种零件和4个乙种零件共需多少分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,A,D,E在同一直线上,BD =AE, BC∥EF, 要使△ABC≌△DEF则需要添加一个适当的条件是______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
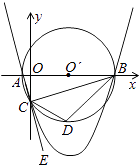
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在同一直线上,△ABD和△BCE都是等边三角形,AE,CD分别与BD,BE交于点F,G,连接FG,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG;④AD⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)

相关试题

