【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
参考答案:
【答案】B
【解析】分析:(1)对应线段的长度即是平移的距离;(2)根据EC的长和△CEG的面积求EG;(3)平移前后,对应点的连线平行且相等;(4)根据平行四边形的面积公式求.
详解:(1)因为点B,E是对应点,且BE=2,所以△ABC平行的距离是2,则①错误;
②根据题意得,13.5×2=(8-2)EG,解得EG=4.5,则②正确;
③因为A,D是对应点,C,F是对应点,所以AD∥CF,则③正确;
④平行四边形ADFC的面积为AB·CF=AB·BE=6×2=12,则④错误.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是( )
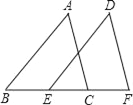
A. AB=DEB. AC=DFC. ∠A=∠DD. ∠ACB=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)当∠OAB=40°时,∠ACB= 度;
(2)随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.

-
科目: 来源: 题型:
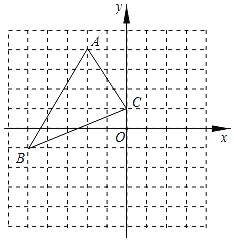
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(﹣2,4),B(﹣5,﹣1),C(0,1),把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形A'B'C'.
(1)画出三角形ABC和平移后A′B′C′的图形;
(2)写出三个顶点A',B',C'的坐标;
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.

(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形面积的最大值。
相关试题

