【题目】如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形面积的最大值。
参考答案:
【答案】
(1)解:将B、C两点的坐标代入得 ![]() ,解得
,解得 ![]() ,
,
所以二次函数的表达式为y=﹣x2+2x+3
(2)解:如图,
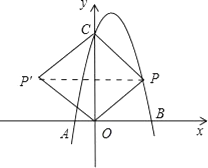
存在点P,使四边形POP′C为菱形.
设P点坐标为(x,﹣x2+2x+3),PP′交CO于E,
若四边形POPC是菱形,则有PC=PO,
连接PP则PE⊥CO于E,
∴OE=CE= ![]() ,
,
∴y= ![]() ,
,
∴-x2+2x+3= ![]() ,
,
解得x1= ![]() ,x2=
,x2= ![]() (不合题意,舍去),
(不合题意,舍去),
∴P点的坐标为( ![]() ,
, ![]() );
);
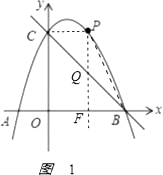
(3)解:如图1,
 ,
,
过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,﹣x2+2x+3)
易得,直线BC的解析式为y=﹣x+3.
则Q点的坐标为(x,﹣x+3).
PQ=﹣x2+3x.
S四边形ABPC=S△ABC+S△BPQ+S△CPQ= ![]() ABOC+
ABOC+ ![]() QPBF+
QPBF+ ![]() QPOF=
QPOF= ![]() ×4×3+
×4×3+ ![]() (﹣x2+3x)×3=﹣
(﹣x2+3x)×3=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
当x= ![]() 时,四边形ABPC的面积最大,
时,四边形ABPC的面积最大,
此时P点的坐标为( ![]() ,
, ![]() ),四边形ABPC面积的最大值为
),四边形ABPC面积的最大值为 ![]() .
.
【解析】(1)利用待定系数法将点C、点B的坐标代入函数解析式即可求出结果。
(2)要使四边形POP′C为菱形,因此根据菱形的对角线互相平分,可得到P点的纵坐标,根据函数值与自变量的对应关系,建立方程可得答案。(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,先求出直线BC的函数解析式,根据两函数解析式设点P的坐标,再表示出点Q的坐标,即可表示出PQ的长,再根据S四边形ABPC=S△ABC+S△BPQ+S△CPQ,建立函数解析式,就可求出此时点P的坐标和四边形面积的最大值。
【考点精析】利用确定一次函数的表达式和二次函数的最值对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)当∠OAB=40°时,∠ACB= 度;
(2)随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.

-
科目: 来源: 题型:
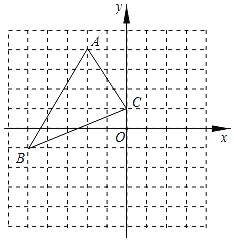
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(﹣2,4),B(﹣5,﹣1),C(0,1),把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形A'B'C'.
(1)画出三角形ABC和平移后A′B′C′的图形;
(2)写出三个顶点A',B',C'的坐标;
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

相关试题

