搜索
【题目】如图，在平面直角坐标系中，△ABC顶点的坐标分别是A（﹣1，3）、B（﹣5，1）、C（﹣2，﹣2）．
（1）画出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′各顶点的坐标；
（2）求出△ABC的面积．
参考答案：
【答案】（1）图形见解析；（2）9.
【解析】
（1）根据网格结构找出点A、B、C关于y轴的 对称点A'、B'、C'的位置，然后顺次连接即可；根据平面直角坐标系写出各点的坐标即可；
（2）利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解．
（1）如图所示，△A′B′C′即为所求，
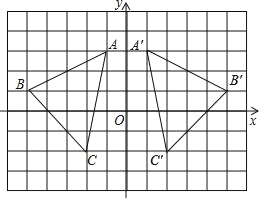
由图知A′（1，3），B′（5，1），C′（2，﹣2）；
（2）△ABC的面积为5×4﹣
×1×5﹣×3×3﹣×2×4＝9．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图(十九)，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框，则任两螺丝的距离之最大值为何？
(A) 5 (B) 6 (C) 7 (D) 10
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G,OC到点E，使OG=2OD,OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG、DE．
n
（1）求证：DE⊥AG；
（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转角(0°<
<360°)得到正方形OE’F’G’，如图2．
①在旋转过程中，当∠OAG’是直角时，求 的度数；
②若正方形ABCD的边长为1，在旋转过程中，求AF’长的最大值和此时 的度数，直接写出结果不必说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点B、E、C、F在同一条直线上，BE＝CF，∠B＝∠DEF，请你添加一个合适的条件，使△ABC≌△DEF，其中不正确条件是（ ）
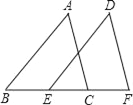
A. AB＝DEB. AC＝DFC. ∠A＝∠DD. ∠ACB＝∠F
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1=40°，求∠BDE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角三角形ABC的直角边AB=6，BC=8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，DE交AC于点G，BE＝2，三角形CEG的面积为13.5，下列结论：
①三角形ABC平移的距离是4； ②EG=4.5；
③AD∥CF； ④四边形ADFC的面积为6．
其中正确的结论是（ ）
A. ①② B. ②③ C. ③④ D. ②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠XOY＝90°，点A、B分别在射线OX、OY上移动（不与点O重合），BE是∠ABY的平分线，BE的反向延长线与∠OAB的平分线相交于点C．
（1）当∠OAB＝40°时，∠ACB＝ 度；
（2）随点A、B的移动，试问∠ACB的大小是否变化？如果保持不变，请给出证明；如果发生变化，请求出变化范围．
相关试题
