【题目】已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)当∠OAB=40°时,∠ACB= 度;
(2)随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.

参考答案:
【答案】(1)45;(2) ∠ACB的大小不发生变化.
【解析】
(1)先利用角平分线得出∠CAB=![]() ∠OAB,∠EBA=
∠OAB,∠EBA=![]() ∠YBA,再利用三角形的外角的性质即可得出结论;
∠YBA,再利用三角形的外角的性质即可得出结论;
(2)先利用角平分线得出∠CAB=![]() ∠OAB,∠EBA=
∠OAB,∠EBA=![]() ∠YBA,再利用三角形的外角的性质即可得出结论.
∠YBA,再利用三角形的外角的性质即可得出结论.
解:(1)∵∠XOY=90°,∠OAB=40°,
∴∠ABY=130°,
∵AC平分∠OAB,BE平分∠YBA,
∴∠CAB=![]() ∠OAB=20°,∠EBA=
∠OAB=20°,∠EBA=![]() ∠YBA=65°,
∠YBA=65°,
∵∠EBA=∠C+∠CAB,
∴∠C=∠EBA﹣∠CAB=45°,
故答案为:45;
(2)∠ACB的大小不变化.
理由:∵AC平分∠OAB,BE平分∠YBA,
∴∠CAB=![]() ∠OAB,∠EBA=
∠OAB,∠EBA=![]() ∠YBA,
∠YBA,
∵∠EBA=∠C+∠CAB,
∴∠C=∠EBA﹣∠CAB=![]() ∠YBA﹣
∠YBA﹣![]() ∠OAB=
∠OAB=![]() (∠YBA﹣∠OAB),
(∠YBA﹣∠OAB),
∵∠YBA﹣∠OAB=90°,
∴∠C=![]() ×90°=45°,
×90°=45°,
即:∠ACB的大小不发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
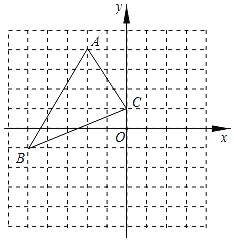
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(﹣2,4),B(﹣5,﹣1),C(0,1),把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形A'B'C'.
(1)画出三角形ABC和平移后A′B′C′的图形;
(2)写出三个顶点A',B',C'的坐标;
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.

(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形面积的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
相关试题

