【题目】如图,在平面直角坐标系中,直线![]() 与x轴、
与x轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,将点
,将点![]() 绕坐标原点
绕坐标原点![]() 顺时针旋转
顺时针旋转![]() 得点
得点![]() ,解答下列问题:
,解答下列问题:
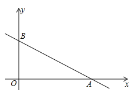
(1)求出点![]() 的坐标,并判断点
的坐标,并判断点![]() 是否在直线l上;
是否在直线l上;
(2)若点![]() 在x轴上,坐标平面内是否存在点
在x轴上,坐标平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出
为顶点的四边形是菱形?若存在,请直接写出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,点
,点![]() 在直线l上,见解析;(2)存在,点
在直线l上,见解析;(2)存在,点![]() 坐标为:
坐标为:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() 或
或![]() .
.
【解析】
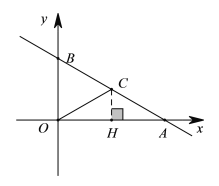
(1)依题意作出点![]() ,过C点作CH⊥OA,旋转性质可得
,过C点作CH⊥OA,旋转性质可得![]() ,由30°直角三角形性质可求出HC=
,由30°直角三角形性质可求出HC=![]() ,OH=3,即可得出C点坐标,将C点坐标代入解析式验证,符合解析式即可判定C在直线l上.
,OH=3,即可得出C点坐标,将C点坐标代入解析式验证,符合解析式即可判定C在直线l上.
即可求解;
(2)分![]() 是菱形的一条边、
是菱形的一条边、![]() 是菱形的一条对角线两种情况,分别根据点平移的规律求解即可.
是菱形的一条对角线两种情况,分别根据点平移的规律求解即可.
解:(1)设将点![]() 绕坐标原点
绕坐标原点![]() 顺时针旋转
顺时针旋转![]() 得点
得点![]() ,
,
直线![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
则点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,OC=OB=
,OC=OB=![]() ,
,
∴![]() ,
,
过C点作CH⊥OA,
∴HC=![]() ,OH=3
,OH=3
点C的坐标为![]() ;
;
∵当x=3时,![]() =
=![]() .
.
∴点![]() 的坐标
的坐标![]() 在直线l上.
在直线l上.
(2)存在,理由:
点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,则
,则![]() ,以
,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形如图所示,
为顶点的四边形是菱形如图所示,
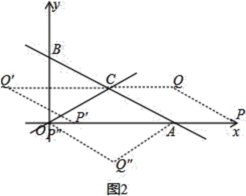
①当![]() 是菱形的一条边时,当点
是菱形的一条边时,当点![]() 在x轴上方,
在x轴上方,
当菱形为![]() 时,则
时,则![]() ,则点
,则点![]() ,
,![]() ;
;
当菱形为![]() 时,点
时,点![]() ,
,![]() ;
;
当点![]() 在x轴下方,
在x轴下方,
同理可得:点![]() ;
;
②当![]() 是菱形的对角线时,
是菱形的对角线时,
设点![]() ,点
,点![]() ,
,
则![]() 的中点即为
的中点即为![]() 的中点,且
的中点,且![]() (即
(即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,
故点![]() ;
;
综上,点![]() 坐标为:
坐标为:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
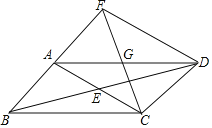
查看答案和解析>>【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
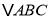 绕点A旋转
绕点A旋转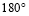 得到
得到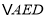 ,
,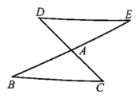
(1)则DE与BC的位置关系是_________,数量关系是_________;
(2)若
 ,则
,则 _________;
_________;(3)若
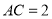 ,
,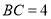 ,
,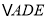 的周长为偶数,则AE的长为_________;
的周长为偶数,则AE的长为_________; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
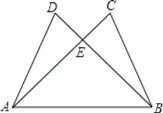
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n
500
1000
1500
2000
2500
优等品频数m
471
946
1426
1898
2370
优等品频率
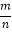
0.942
0.946
0.951
0.949
0.948
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
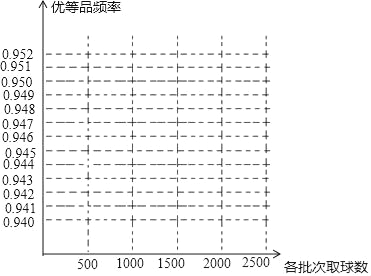
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为
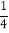 ,求取出了多少个黑球?
,求取出了多少个黑球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边
的边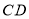 在正方形
在正方形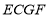 的边
的边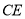 上,连接
上,连接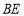 ,
,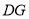 ,
,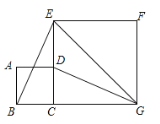
(1)求证:
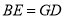 ;
;(2)若
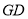 平分
平分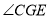 ,
,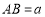 ,
,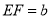 ,求
,求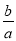 的值.
的值.(3)连接
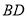 ,若
,若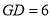 ,求
,求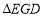 与
与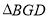 面积的和.
面积的和.
相关试题

