【题目】如图是 2019 年五月的月历,“T”型、“田”型两个阴影图形分别覆盖其中四个方格(可以重叠覆盖),设“T”型阴影覆盖的最小数字为 a,四个数字之和为 S1,“田”型阴影覆盖的最小数字为 b,四个数字之和为 S2.
(1) S1 的值能否为 50?若能,求 a 的值;若不能,说明理由;
(2)S1+ S2 值能否为 35,若能,求 a,b 的值;若不能,说明理由;
(3)若 S1+ S2=43,求 S1-S2 的值为 (直接写结果).
参考答案:
【答案】(1)不能,理由见解析;(2)能,a=1,b=1;(3)-13或-5.
【解析】
(1)根据日历中的规律可表示出数字,从而表示出S1,然后根据S1=50列式计算,最后进行判断即可;
(2)根据日历中的规律可表示出数字,从而表示出S2,然后根据S1+ S2=35列式计算,得到a、b;
(3)根据S1+ S2=43列式计算,得到a、b,再计算S1-S2,最后代入a、b计算得到结果即可.
解:(1)不能,理由如下:
由题知,“T”型阴影覆盖的最小数字为 a,则其他三个数字分别为:a+1、a+2、a+8,
∴![]() ,
,
令S1=50,即![]() ,得
,得![]() ,
,
因为a不可能为分数,故S1不能为50.
(2)能.由题知,“田”型阴影覆盖的最小数字为 b,则其他三个数字分别为:b+1、b+7、b+8,
∴![]() ,
,
∴![]() ,
,
令![]() ,即
,即![]() ,得
,得![]() ,
,
∵a、b均为大于等于1且小于等于31的整数,
∴a=1,b=1.
(3)令![]() ,即
,即![]() ,得
,得![]() ,
,
∵a、b均为大于等于1且小于等于31的整数,
∴有三种情况:①![]() ,②
,②![]() ,③
,③![]() (构不成“T”型,故舍去),
(构不成“T”型,故舍去),
又![]() ,
,
∴当a=1,b=3时,S1-S2=-13;当a=2,b=2时,S1-S2=-5;
故S1-S2的值为-13或-5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
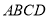 ,长
,长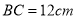 ,宽
,宽 ,
, 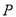 、
、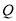 分别是
分别是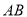 、
、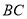 上运动的两点。若
上运动的两点。若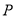 自点
自点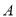 出发,以
出发,以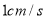 的速度沿
的速度沿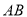 方向运动,同时,
方向运动,同时, 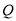 自点
自点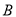 出发以
出发以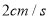 的速度沿
的速度沿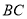 方向运动,则经过____________秒,以
方向运动,则经过____________秒,以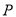 、
、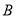 、
、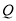 为顶点的三角形与
为顶点的三角形与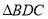 相似。
相似。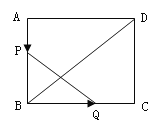
-
科目: 来源: 题型:
查看答案和解析>>【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①,图②都是4×6的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,且点A,B均在格点上.

(1)在图①中以AB为对角线画出一个矩形,使矩形的另外两个顶点也在格点上,且所画的矩形不是正方形;
(2)在图②中以AB为对角线画出一个菱形,使菱形的另外两个顶点也在格点上,且所画的菱形不是正方形;
(3)图①中所画的矩形的面积为 ;图②中所画的菱形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有理数 a,b,c 分别对应数轴上的点 A,B,C,若a 2
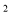 |b 4| 0 ,关于 x、y 的单项式3(c 3)x
|b 4| 0 ,关于 x、y 的单项式3(c 3)x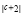 y
y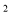 与 y
与 y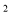 x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.

(1)求 a,b,c 的值;
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动:第一回合,从点 C 到点 B 到点 A 回到点 C;第二回合,从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C;第三回合,从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……,如此循环下去,若第 t 秒时满足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的条件下,P 点第一次从 C 点出发的同时,数轴上的动点 M、N 分别从 A 点和 B 点向右运动,速度分别为每秒 1 个单位长度和每秒 2 个单位长度,P 点完成第一个回合后停止在 C 点,当 MP=2MN 时, t 的值是 (直接填答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
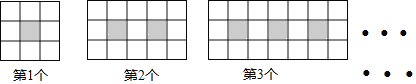
-
科目: 来源: 题型:
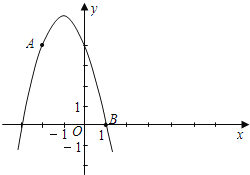
查看答案和解析>>【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
相关试题

