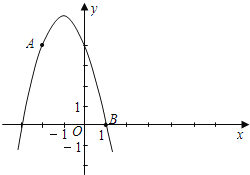
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
参考答案:
【答案】(1)m=﹣![]() ,n=4 (2)y=﹣
,n=4 (2)y=﹣![]() (x﹣4)2+
(x﹣4)2+![]() (3)D(3,0)或(
(3)D(3,0)或(![]() ,0).
,0).
【解析】(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形AA′B′B一定为平行四边形,若四边形AA′B′B为菱形,那么必须满足AB=BB′,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AB′的解析式,联立平移后的抛物线对称轴,可得到C点的坐标,进而可求出AB、BC、AC、B′C的长;在(2)题中已经证得AB=BB′,那么∠BAC=∠BB′C,即A、B′对应,若以点B′、C、D为顶点的三角形与△ABC相似,可分两种情况考虑:①∠B′CD=∠ABC,此时△B′CD∽△ABC,②∠B′DC=∠ABC,此时△B′DC∽△ABC;
根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的BD长,进而可求得D点的坐标.
解:(1)由于抛物线经过A (﹣2,4)和点B (1,0),则有:
![]() ,解得
,解得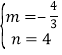 ;
;
故m=﹣![]() ,n=4.
,n=4.
(2)由(1)得:y=﹣![]() x2﹣
x2﹣![]() x+4=﹣
x+4=﹣![]() (x+1)2+
(x+1)2+![]() ;
;
由A (﹣2,4)、B (1,0),可得AB=![]() =5;
=5;
若四边形A A′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=﹣![]() (x+1﹣5)2+
(x+1﹣5)2+![]() =﹣
=﹣![]() (x﹣4)2+
(x﹣4)2+![]() .
.
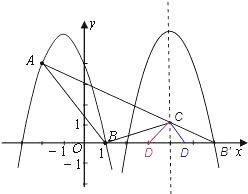
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(﹣2,4),B′(6,0),
∴直线AB′:y=﹣![]() x+3;
x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3![]() ,B′C=
,B′C=![]() ,BC=
,BC=![]() ;
;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=3,
,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=
,B′D=![]() ,
,
此时D(![]() ,0);
,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(![]() ,0).
,0).
“点睛”此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质、相似三角形的判定和性质等知识;(3)题中,在相似三角形的对应角和对应边不确定的情况下,一定要分类讨论,以免漏解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是 2019 年五月的月历,“T”型、“田”型两个阴影图形分别覆盖其中四个方格(可以重叠覆盖),设“T”型阴影覆盖的最小数字为 a,四个数字之和为 S1,“田”型阴影覆盖的最小数字为 b,四个数字之和为 S2.

(1) S1 的值能否为 50?若能,求 a 的值;若不能,说明理由;
(2)S1+ S2 值能否为 35,若能,求 a,b 的值;若不能,说明理由;
(3)若 S1+ S2=43,求 S1-S2 的值为 (直接写结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有理数 a,b,c 分别对应数轴上的点 A,B,C,若a 2
 |b 4| 0 ,关于 x、y 的单项式3(c 3)x
|b 4| 0 ,关于 x、y 的单项式3(c 3)x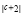 y
y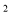 与 y
与 y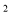 x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.

(1)求 a,b,c 的值;
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动:第一回合,从点 C 到点 B 到点 A 回到点 C;第二回合,从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C;第三回合,从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……,如此循环下去,若第 t 秒时满足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的条件下,P 点第一次从 C 点出发的同时,数轴上的动点 M、N 分别从 A 点和 B 点向右运动,速度分别为每秒 1 个单位长度和每秒 2 个单位长度,P 点完成第一个回合后停止在 C 点,当 MP=2MN 时, t 的值是 (直接填答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
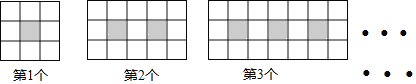
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为⊙O的直径,B是⊙O外一点,AB交⊙O于E点,过E点作⊙O的切线,交BC于D点,DE=DC,作EF⊥AC于F点,交AD于M点。
求证:(1)BC是⊙O的切线; (2)EM=FM。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.

(1)汽车行驶 h后加油,加油量为 L;
(2)求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;
(3)如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

相关试题

