【题目】已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE。 求证:AC-AB=2BE.

参考答案:
【答案】见解析.
【解析】
延长BE交AC于M,利用三角形内角和定理,得出∠3=∠4,AB=AM,∴AC-AB=AC-AM=CM.再利用∠4是△BCM的外角,再利用等腰三角形对边相等,CM=BM利用等量代换即可求证.
证明:延长BE交AC于M
∵BE⊥AE,
∴∠AEB=∠AEM=90°
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°-∠1
同理,∠4=90°-∠2
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM
∵BE⊥AE,
∴BM=2BE,
∴AC-AB=AC-AM=CM,
∵∠4是△BCM的外角
∴∠4=∠5+∠C
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5
∴3∠C=∠4+∠5=2∠5+∠C
∴∠5=∠C
∴CM=BM
∴AC-AB=BM=2BE.
-
科目: 来源: 题型:
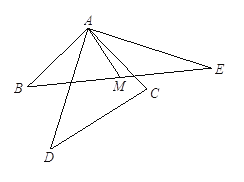
查看答案和解析>>【题目】如图所示,
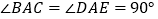 ,
,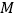 是
是 的中点,
的中点,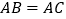 ,
,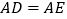 ,求证
,求证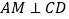 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:BH∥DG;
(2)求证:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求线段CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
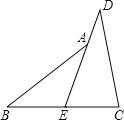
查看答案和解析>>【题目】如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,
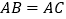 ,BD平分∠ABC,BC上有动点P.
,BD平分∠ABC,BC上有动点P.(1)DP⊥BC时(如图1),求证:
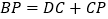 ;
;(2)DP平分∠BDC时(如图2),BD、CD、CP三者有何数量关系?
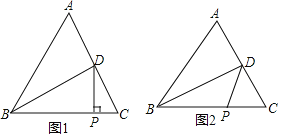
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 的中点,要使四边形
的中点,要使四边形 是矩形,则四边形
是矩形,则四边形 只需要满足一个条件是( )
只需要满足一个条件是( )
A.四边形
 是梯形B.四边形
是梯形B.四边形 是菱形
是菱形C.对角线
 D.
D.
相关试题

