【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:BH∥DG;
(2)求证:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求线段CG的长.

参考答案:
【答案】(1)见解析;(2)见解析;(3)① 4;②CG=3 cm
【解析】
(1)根据折叠的性质可得![]() ,再根据平行线的性质得到∠1=∠2,故可求解;
,再根据平行线的性质得到∠1=∠2,故可求解;
(2)根据矩形的性质及ASA即可证明△BEH≌△DFG;
(3)①先根据勾股定理求出BD,再得到DF=CD=8,即可求出BF的长;
②由图形翻折变换的性质得出CG=FG,设CG=x,则BG=8x,再利用勾股定理即可求出x的值.
解:(1)由折叠可知:![]() .
.
在矩形ABCD中,AB//CD,
∴∠ABD=∠BDC.
∴∠1=∠2.
∴BH//DG.

(2)在矩形ABCD中,
∴∠A=∠C,AB=CD.
由折叠可知:AB=BE,CD=DF,∠3=∠A,∠4=∠C.
∴BE=DF,∠3=∠4.
在△BEH和△DFG中,

∴△BEH≌△DFG.
(3)①∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD=![]()
∵由(2)知,FD=CD,CG=FG,
∴BF=106=4cm,
故答案为:4;
②设CG=x cm,则FG=x cm,BG=(8-x)cm,
在Rt△BGF中,BG2=BF2+FG2,
即![]()
解得x=3
即CG=3 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.

(1)学校采用的调查方式是 ;学校共选取了 名学生;
(2)补全统计图中的数据:条形统计图中羽毛球 人、乒乓球 人、其他 人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
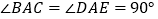 ,
,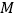 是
是 的中点,
的中点,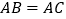 ,
,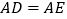 ,求证
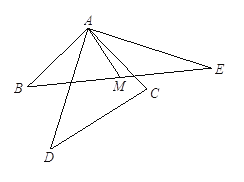
,求证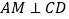 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE。 求证:AC-AB=2BE.

-
科目: 来源: 题型:
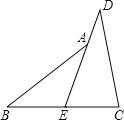
查看答案和解析>>【题目】如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD .
相关试题

