搜索
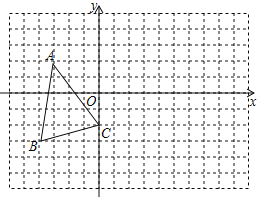
【题目】如图，已知在直角坐标系中，
的顶点都在网络格上:
（1）请写出点
的坐标；
（2）先画出先向
轴正方向平移
个单位长度，得到
;请写出点
的坐标．
参考答案：
【答案】（1）（-3，2），（-4，-3），（0，-2） （2）图见解析；（1，2），（0，-3），（4，-2）
【解析】
（1）根据平面直角坐标系和网格图可得出点
的坐标；
（2）把点分别沿
轴正方向平移
个单位长度，得到
，连接三点得到
，写出三顶点坐标即可．
（1）根据图形可知，点A、B、C的坐标分别为：（-3，2），（-4，-3），（0，-2），
故答案为：（-3，2），（-4，-3），（0，-2）；
（2）把点分别沿轴正方向平移个单位长度后得到，则三个顶点的坐标分别为：（1，2），（0，-3），（4，-2），
故答案为：（1，2），（0，-3），（4，-2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 我们定义：如图1、图2、图3，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′，当α+β＝180°时，我们称△AB'C′是△ABC的“旋补三角形”，△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”．
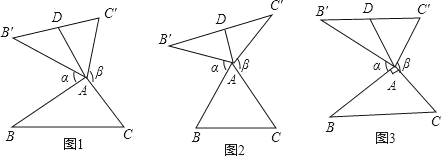
（1）①如图2，当△ABC为等边三角形时，“旋补中线”AD与BC的数量关系为：AD＝ BC；
②如图3，当∠BAC＝90°，BC＝8时，则“旋补中线”AD长为 ．
（2）在图1中，当△ABC为任意三角形时，猜想“旋补中线”AD与BC的数量关系，并给予证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，CD为⊙O的直径，弦AB交CD于点E，连接BD、OB．
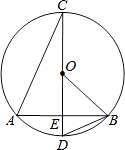
（1）求证：△AEC∽△DEB；
（2）若CD⊥AB，AB=8，DE=2，求⊙O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某地方政府决定在相距50km的A、B两站之间的公路旁E点，修建一个土特产加工基地，且使C、D两村到E点的距离相等，已知DA⊥AB于A，CB⊥AB于B，DA=30km，CB=20km，那么基地E应建在离A站多少千米的地方？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图(1)所示，∠AOB、∠COD都是直角．
(1)试判断∠AOC与∠BOD的大小关系，并说明理由；
(2)若∠BOC=60°，求∠AOD的度数；
(3)猜想∠AOD与∠BOC在数量上是相等，互余，还是互补的关系，并说明理由；
(4)当∠COD绕着点O旋转到图(2)所示位置时，你在(3)中的猜想还成立吗？请用你所学的知识加以说明．
-
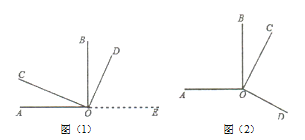
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，点 D，E 分别在边 AC，AB 上，BD 与 CE 交于点 O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC．
(1)上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形，写出证明过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】运算能力是一项重要的数学能力．兵老师为帮助学生诊断和改进运算中的问题，对全班学生进行了三次运算测试（每次测验满分均为100分）．小明和小军同学帮助兵老师统计了某数学小组5位同学（A，B，C，D，E，F）的三次测试成绩，小明在下面两个平面直角坐标系里描述5位同学的相关成绩．小军仔细核对所有数据后发现，图1中所有同学的成绩坐标数据完全正确，而图2中只有一个同学的成绩纵坐标数据有误．以下说法中：①A同学第一次成绩50分，第二次成绩40分，第三次成绩60分；②B同学第二次成绩比第三次成绩高；③D同学在图2中的纵坐标是有误的；④E同学每次测验成绩都在95分以上．其中合理的是（ ）
A.①②③B.①②④C.①③④D.②③④
相关试题
