【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

参考答案:
【答案】20千米
【解析】试题分析:由勾股定理两直角边的平方和等于斜边的平方即可求,即在直角三角形DAE和直角三角形CBE中利用斜边相等两次利用勾股定理得到AD2+AE2=BE2+BC2,设AE为x,则BE=10﹣x,将DA=8,CB=2代入关系式即可求得.
解:设基地E应建在离A站x千米的地方.
则BE=(50﹣x)千米
在Rt△ADE中,根据勾股定理得:AD2+AE2=DE2
∴302+x2=DE2…(3分)
在Rt△CBE中,根据勾股定理得:CB2+BE2=CE2
∴202+(50﹣x)2=CE2
又∵C、D两村到E点的距离相等.
∴DE=CE∴DE2=CE2
∴302+x2=202+(50﹣x)2
解得x=20
∴基地E应建在离A站多少20千米的地方.
-
科目: 来源: 题型:
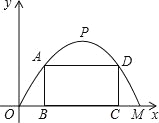
查看答案和解析>>【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角的平分线上的点到角的两边的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC.
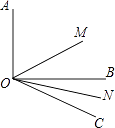
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的数为4,那么到点A的距离等于5个单位长度的点所表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+a=a2B. 6a3﹣5a2=a
C. (2x5)2=4x10D. a6÷a2=a3
相关试题

