【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当点A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A.![]()
B.2 ![]()
C.3
D.2 ![]()
参考答案:
【答案】A
【解析】解:∵∠ACB=90°,∠ABC=30°,AC=2,
∴∠A=90°-∠ABC=90°-30°=60°,AB=2AC=4,CB=2![]()
∵△ABC绕点C顺时针旋转得△A1B1C,
∴A1C=AC,
∴△A1AC是等边三角形,
∴A1C=AC=A1A=2,
∴∠B1CB=∠ACA1=60°,
∵CB=CB1 ,
∴△CB1B是等边三角形,
∴B1B=2![]() ,BA1=2,∠A1B1B=90°
,BA1=2,∠A1B1B=90°
∵BB1的中点D,
∴BD=DB1=![]()
A1D=![]() =
=![]() =
=![]()
故答案为:A先根据题意证明△A1AC和△CB1B是等边三角形,,再证明△A1BD是直角三角形,然后根据勾股定理求出A1D的长即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,点D在AB延长线上,且∠BCD=∠A.
(1)求证:DC是⊙O的切线;
(2)若∠A=30°,AC=2
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
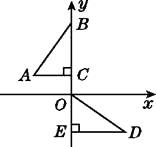
查看答案和解析>>【题目】如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是等腰直角三角形,直线BD∥OA,OB=OA=1,P是线段AB上一动点,过P点作MN∥OB,分别交OA、BD于M、N,PC⊥PO,交BD于点C.
(1)求证:OP=PC;
(2)当点C在射线BN上时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线BN上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形时的PM的值;如果不可能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.

(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形属于因式分解的是()
A.(x+2)(x-3)=x2-x-6B.6xy=2x2·3y3
C.x2+2x+1=x(x2+2)+1D.x2-9=(x-3)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x-3与一个多项式的乘积为x2+x-12,则这个多项式为()
A.x+4B.x-4C.x-9D.x+6
相关试题

