【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)求证:AC2=COCP;
(3)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.

参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)⊙O的直径为![]() .
.
【解析】试题分析:(1)连结OA、AD,如图,利用圆周角定理得到∠CAD=90°,∠ADC=∠B=60°,则∠ACD=30°,再利用AP=AC得到∠P=∠ACD=30°,接着根据圆周角定理得∠AOD=2∠ACD=60°,然后根据三角形内角和定理可计算出∠OAP=90°,于是根据切线的判定定理可判断AP与 O相切;
(2)通过△ACO∽△PCA,得到![]() =
=![]() ,由于AC=AP于是得到结论;
,由于AC=AP于是得到结论;
(3)连接AD,证得△AOD是等边三角形,得到∠OAD=60°,求得AD=PD=![]() ,得到OD=
,得到OD=![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)连结OA、AD,如图,

∵CD为直径,
∴∠CAD=90°,
∵∠ADC=∠B=60°,
∴∠ACD=30°,
∵AP=AC,
∴∠P=∠ACD=30°,
∵∠AOD=2∠ACD=60°,
∴∠OAP=180°﹣60°﹣30°=90°,
∴OA⊥PA,
∴AP与⊙O相切;
(2)∵∠P=∠ACP=∠CAO=30°,
∴△ACO∽△PCA,
∴![]() =
=![]() ,
,
∵AC=AP
∴AC2=CO.CP;
(3)∵AO=DO,∠ADC=60°,
∴△AOD是等边三角形,
∴∠OAD=60°,
∴∠PAD=30°,
∴∠P=∠PAD,
∴AD=PD=![]() ,
,
∴OD=![]() ,
,
∴⊙O的直径CD=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林的门票每张10元,一次使用,考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年).年票分A、B、C三类:A类年票每张120元,持票者进入园林时,无需再用门票;B类年票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类年票每张40元,持票者进入该园林时,需再购买门票,每次3元.
(1)如果只选择一种购买门票的方式,并且计划在一年中用不多于80元花在该园林的门票上,试通过计算,找出可进入该园林次数最多的购票方式,
(2)一年中进入该园林至少超过______________次时,购买A类年票最合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2) 
(3)
 (4)
(4) 
【答案】(1)
 ;(2)
;(2)  ;(3)
;(3)  ; (4)
; (4) 
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=

=
 ;
;(2)原式=

=

=
 ;
;(3)原式=

=

=

=
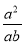
=
 ;
;(4)原式=
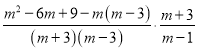
=

=
 .
.点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20【题目】解分式方程:
(1)
 (2)
(2) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的
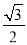 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:  ≈2.449,
≈2.449, 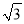 ≈1.732,
≈1.732, 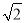 ≈1.414)
≈1.414)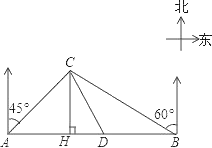
-
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程:
(1)
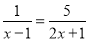 (2)
(2) 
【答案】(1)
 ;(2)x=
;(2)x=
【解析】试题分析:(1)两边乘以(x-1)(2x+1)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可;
(2)两边乘以(x+2)(x-2)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可.
试题解析:
解:(1)两边乘以(x-1)(2x+1)去分母得:2x+1=5(x-1),
解得:x=2,
当x=2时,(x-1)(2x+1)≠0,
∴原分式方程的解为x=2;
(2)两边乘以(x+2)(x-2)去分母得:(x-2)2-3=(x+2)(x-2),
解得:x=
 ,
,当x=
 时,(x+2)(x-2)≠0,
时,(x+2)(x-2)≠0,所以原分式方程的解为x=
 .
.【题型】解答题
【结束】
21【题目】先化简,再求值
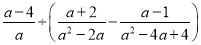 ,其中
,其中 的值从不等式组
的值从不等式组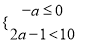 的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
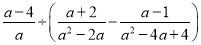 ,其中
,其中 的值从不等式组
的值从不等式组 的整数解中选取.
的整数解中选取.【答案】(a-2)2.
【解析】试题分析:根据分式的减法和除法可以化简题目中的式子,然后在不等式组
 的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.试题解析:
解:原式=
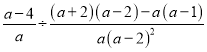
=
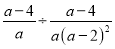
=
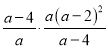
=(a-2)2,
由不等式组
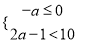 得,0≤a<5.5,
得,0≤a<5.5,∴当a=1时,原式=(1-2)2=1.
点睛:本题考查分式的化简求值、一元一次不等式组的整数解,解答本题的关键是明确分式化简求值的方法,会求一元一次不等式组的解集.
【题型】解答题
【结束】
22【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
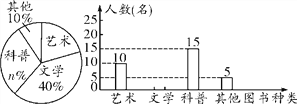
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)请根据以上信息补全条形统计图;
(4)根据抽样调查的结果,请你估计该校1000名学生中有多少学生最喜欢科普类图书.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
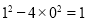 ①;
①; 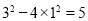 ②;
②; 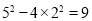 ③……
③……根据上述规律解决下列问题:
(1)完成第四个等式: ;
(2)猜想第
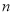 个等式(用含
个等式(用含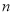 的式子表示),并证明其正确性.
的式子表示),并证明其正确性.
相关试题

