【题目】某园林的门票每张10元,一次使用,考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年).年票分A、B、C三类:A类年票每张120元,持票者进入园林时,无需再用门票;B类年票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类年票每张40元,持票者进入该园林时,需再购买门票,每次3元.
(1)如果只选择一种购买门票的方式,并且计划在一年中用不多于80元花在该园林的门票上,试通过计算,找出可进入该园林次数最多的购票方式,
(2)一年中进入该园林至少超过______________次时,购买A类年票最合算.
参考答案:
【答案】(1) 购买C类年票可进入该园林的次数最多;(2)30.
【解析】
(1)根据题意分别求出直接购买门票、购买A类年票、购买B类年票、购买C类年票的次数,比较即可解答;(2)设一年中进入该园林至少超过x次时,购买A类年票比较合算,根据题意列出不等式60+2x≥120,解不等式即可求解.
(1)解:①若直接购买门票,设可进入x次,根据题意,得
10x≤80
解得x≤8
最多可进入该园林8次
②若购买A类年票
∵120>80
∴不能购买A类年票
③若购买B类年票,设可进入y次,根据题意,得
60+2y≤80
解得y≤10
∴最多可进入该园林10次.
④若购买C类年票,设可进入m次,根据题意,得
40+3m≤80
解得m≤![]()
∵m是整数,所以m最大取13
∴最多可进入该园林13次
综上:∵8<10<13
∴购买C类年票可进入该园林的次数最多
(2) 设一年中进入该园林至少超过x次时,购买A类年票比较合算,根据题意得,
60+2x≥120,
解得x≥30.
∴一年中进入该园林至少超过30次时,购买A类年票比较合算.
故答案为:30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线
 (x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )
(x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )
A.
 B.
B.  C. 3 D. 6
C. 3 D. 6【答案】A
【解析】试题分析:∵点D为平行四边形ABCO的对角线交点,双曲线y=
 (x<0)经过点D,AC⊥y轴,
(x<0)经过点D,AC⊥y轴,∴S平行四边形ABCO=4S△COD=4×
 ×|
×| |=
|= .
.故选A.
点睛:本题考查了反比例函数系数k的几何意义以及平行四边形的性质,根据平行四边形的性质结合反比例函数系数k的几何意义,找出S平行四边形ABCO=4S△COD=2|k|是解题的关键.
【题型】单选题
【结束】
9【题目】如果分式
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是_____________.
的取值范围是_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD不添加任何字母和数字,请你再添加一个条件∠1=∠2成立(要求给出三个答案),并选择其中一种情况加以证明.

条件1:________________________________;
条件2:________________________________;
条件3:________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx(k<0)与双曲线
 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
【答案】-6
【解析】试题分析:∵点A(x1,y1),B(x2,y2)是双曲线y=
 上的点,
上的点,∴x1y1=x2y2=-3①,
∵直线y=kx(k<0)与双曲线y=
 交于点A(x1,y1),B(x2,y2)两点,
交于点A(x1,y1),B(x2,y2)两点,∴x1=-x2,y1=-y2②,
∴原式=-3x1y1+5x2y2=9-15=-6.
故答案为:-6.
点睛:本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.
【题型】填空题
【结束】
15【题目】A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了 50%,而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h,则根据题意可列方程为 _____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2) 
(3)
 (4)
(4) 
【答案】(1)
 ;(2)
;(2)  ;(3)
;(3)  ; (4)
; (4) 
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=

=
 ;
;(2)原式=

=

=
 ;
;(3)原式=

=

=

=
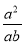
=
 ;
;(4)原式=
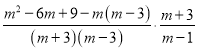
=

=
 .
.点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20【题目】解分式方程:
(1)
 (2)
(2) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的
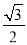 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:  ≈2.449,
≈2.449, 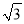 ≈1.732,
≈1.732, 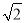 ≈1.414)
≈1.414)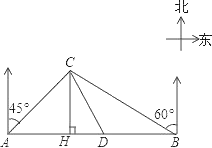
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)求证:AC2=COCP;
(3)若PD=
 ,求⊙O的直径.
,求⊙O的直径.
相关试题

