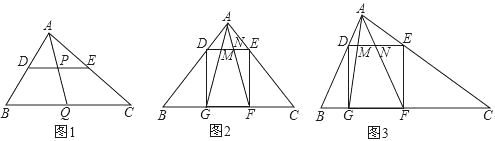
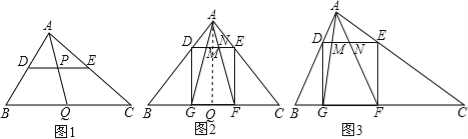
【题目】(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证: ![]() ;
;
(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM·EN.
参考答案:
【答案】(1)证明见解析;(2)MN=![]() .证明见解析.
.证明见解析.
【解析】试题分析:(1)可证明△ADP∽△ABQ,△ACQ∽△ADP,从而得出![]() =
=![]() ;
;
(2)①根据三角形的面积公式求出BC边上的高![]() ,根据△ADE∽△ABC,求出正方形DEFG的边长
,根据△ADE∽△ABC,求出正方形DEFG的边长![]() ,根据
,根据![]() 等于高之比即可求出MN;
等于高之比即可求出MN;
②可得出△BGD∽△EFC,则DGEF=CFBG;又由DG=GF=EF,得GF2=CFBG,再根据(1)![]() =
=![]() =
=![]() ,从而得出答案.
,从而得出答案.
(1)证明:在△ABQ和△ADP中,
∵DP∥BQ,
∴△ADP∽△ABQ,
∴![]() =
=![]() ,
,
同理在△ACQ和△APE中,
![]() =
=![]() ,
,
∴![]() =
=![]() .
.
(2)①作AQ⊥BC于点Q.
∵BC边上的高AQ=![]() ,
,
∵DE=DG=GF=EF=BG=CF
∴DE:BC=1:3
又∵DE∥BC,
∴AD:AB=1:3,
∴AD=![]() ,DE=
,DE=![]() ,
,
∵DE边上的高为![]() ,MN:GF=
,MN:GF=![]() :
:![]() ,
,
∴MN:![]() =
=![]() :
:![]() ,
,
∴MN=![]() .
.
故答案为:![]() .
.
②证明:∵∠B+∠C=90°∠CEF+∠C=90°,
∴∠B=∠CEF,
又∵∠BGD=∠EFC,
∴△BGD∽△EFC,
∴![]() =
=![]() ,
,
∴DGEF=CFBG,
又∵DG=GF=EF,
∴GF2=CFBG,
由(1)得![]() =
=![]() =
=![]() ,
,
∴![]() ×
×![]() =
=![]()
![]() ,
,
∴(![]() )2=
)2=![]()
![]() ,
,
∵GF2=CFBG,
∴MN2=DMEN.
-
科目: 来源: 题型:
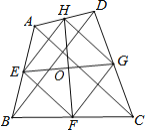
查看答案和解析>>【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.
-
科目: 来源: 题型:
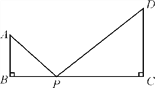
查看答案和解析>>【题目】如图,已知AB⊥BC于点B,CD⊥BC于点C,AB=4,CD=6,BC=14,P为BC边上一点,试问BP为何值时,以A,B,P为顶点的三角形与以P,C,D为顶点的三角形相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
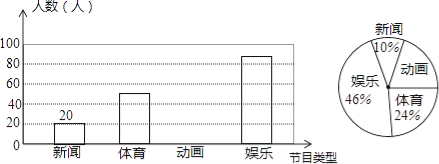
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.
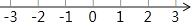
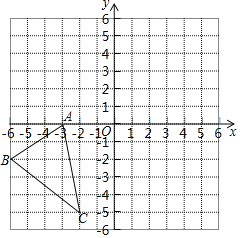
(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )

A. 20
 米 B. (20
米 B. (20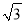 -8)米 C. (20
-8)米 C. (20 -28)米 D. (20
-28)米 D. (20 -20)米
-20)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
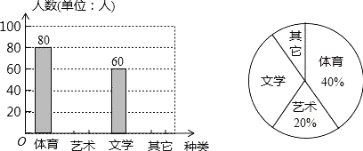
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
相关试题

