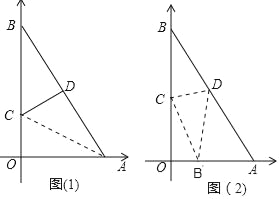
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标.
(2)若折叠后点B落在边OA上的点为B′,是否存在点B′,使得四边形BCB′D是菱形?若存在,请说明理由并求出菱形的边长;若不存在,请说明理由.

参考答案:
【答案】(1)C(0,1.5);(2)存在点B',使得四边形BCB'D是菱形,此时菱形的边长为20﹣8![]() .
.
【解析】
(1)折叠后使点B与点A重合,则C在AB的中垂线上,Rt△AOC中利用勾股定理即可得到方程,求得C的坐标;
(2)当B'C∥AB(或B'D∥BO)时,四边形BCB'D是菱形,则△OB'C∽△OAB,依据相似三角形的对应边的比相等即可求得B′C的长度,然后根据△AB'D∽△AOB,即可求得B′D的长.从而证得B'C=BC=B'D=BD.
(1)设C(0,m),(m>0),
则CO=m,
BC=AC=(4﹣m),
在Rt△AOC中,有(4﹣m)2﹣m2=4,
整理得,12m=8,
∴m=1.5,
∴C(0,1.5);
(2)存在,当B'C∥AB(或B'D∥BO)时,四边形BCB'D是菱形,
∵∠AOB=90°,OA=2,OB=4,
∴AB=2![]() ,
,
∵B'C∥AB,
∴△OB'C∽△OAB,
∴![]() ,
,
设B'C=BC=x,则![]() ,
,
解得,x=2,
∵B'C∥AB,
∴∠CBD+∠BCB'=180°,
又∵∠CBD=∠CB'D,
∴∠CB'D+∠BCB'=180°,
∴B'D∥BO,
∴△AB'D∽△AOB,
∴![]() ,
,
设B'D=BD=y,
∴![]() ,
,
解得:y=20﹣8![]() ,
,
∴B'C=BC=B'D=BD,
∴四边形BCB'D是菱形,
∴存在点B',使得四边形BCB'D是菱形,此时菱形的边长为20﹣8![]() .
.
-
科目: 来源: 题型:
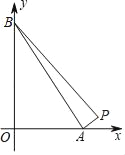
查看答案和解析>>【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号
月租费(元)
免费时间(分)
超过免费时间的通话费(元/分)
一
10
0
0.20
二
30
80
0.15
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
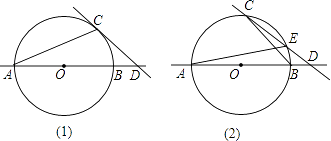
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.

(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
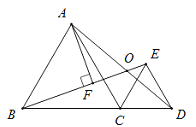
A. 1 B.
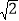 C.
C. 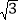 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
相关试题

