【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线y=x2+bx+c经过A、C两点.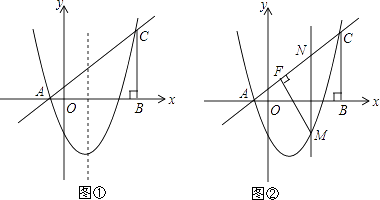
(1)求抛物线的解析式及其顶点坐标;
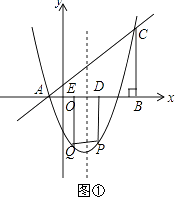
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P,Q分别向x轴作垂线,垂足为点D,E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
参考答案:
【答案】
(1)
解:由已知得:A(﹣1,0)、C(4,5),
∵二次函数y=x2+bx+c的图象经过点A(﹣1,0)C(4,5),
∴ ![]() ,
,
解得 ![]() .
.
∴抛物线解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4)
(2)
解:由(1)知抛物线的对称轴为直线x=1,
设点P为(t,t2﹣2t﹣3),﹣1<t<3
∵P、Q为抛物线上的对称点,
∴PQ=2|t﹣1|,
当t>1时,d=2[2(t﹣1)+(﹣t2+2t+3)]=﹣2t2+8t+2=﹣2(t﹣2)2+10,
∵﹣2<0,
∴当t=2时,d有最大值为10,即P(2,﹣3);
当t<1时,由抛物线的对称性得,点P为(0,﹣3)时,d有最大值10,;
综上,当P为(0,﹣3)或(2,﹣3)时,d有最大值10
(3)
解:过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°,
∵MF⊥AC,
∴FH= ![]() MN,
MN,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵A(﹣1,0,C(4,5),
∴直线AC的解析式为y=x+1,
设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,
由MN∥BC得,N(m,m+1),
∴MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,
当 ![]() =
= ![]() 时,则3MN=4CG,即3(﹣m2+3m+4)=4(4﹣m),
时,则3MN=4CG,即3(﹣m2+3m+4)=4(4﹣m),
解得m1= ![]() ,m2=4(舍去),
,m2=4(舍去),
∴M( ![]() ,﹣
,﹣ ![]() ),
),
当 ![]() =
= ![]() 时,则2MN=6CG,即2(﹣m2+3m+4)=6(4﹣m),
时,则2MN=6CG,即2(﹣m2+3m+4)=6(4﹣m),
解得m3=2,m4=4(舍去),
∴M(2,﹣3).
综上,当M的坐标为( ![]() ,﹣
,﹣ ![]() )或(2,﹣3)时,MN将△MFC的面积分成2:3两部分.
)或(2,﹣3)时,MN将△MFC的面积分成2:3两部分.
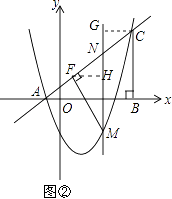
【解析】(1)利用待定系数法即可求得抛物线的解析式,进而转化成顶点式,求得顶点坐标即可;(2)设点P为(t,t2﹣2t﹣3),﹣1<t<3,因为对称轴x=1,所以PQ=2|t﹣1|,然后分三种情况讨论即可求得;(3)过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°,进而求得FH= ![]() MN,从而得出
MN,从而得出 ![]() =
= ![]() =
= ![]() ,根据A、C的坐标求得直线AC的解析式为y=x+1,设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,由MN∥BC得N(m,m+1),求得MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,然后分两种情况:当
,根据A、C的坐标求得直线AC的解析式为y=x+1,设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,由MN∥BC得N(m,m+1),求得MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,然后分两种情况:当 ![]() =
= ![]() 时,则3MN=4CG;当
时,则3MN=4CG;当 ![]() =
= ![]() 时,则2MN=6CG;列出关于m的方程,解方程即可求得M的坐标.
时,则2MN=6CG;列出关于m的方程,解方程即可求得M的坐标.
【考点精析】解答此题的关键在于理解二次函数的概念的相关知识,掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数,以及对二次函数的图象的理解,了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC=12,面积为24,△ABE是等边三角形,若点P在对角线AC上移动,则PD+PE的最小值为( )

A. 4 B. 4
 C.
C.  D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.
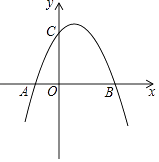
(1)求A,B,C三点的坐标?
(2)求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A,B,C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形EFGH在边长为4的正方形ABCD所在平面上移动,始终保持EF//AB,CK=1.线段KG的中点为M,DH的中点为N,则线段MN的长为 ( ).

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.求作:菱形AMBN,使得其对角线分别等于b和2a.
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.求作:菱形AMBN,使得其对角线分别等于b和2a.
小军的作法如下:
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于
 AB的长为半径,
AB的长为半径,在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于
 AB的长为半径,
AB的长为半径,在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是_______________________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)已知:关于
 的方程
的方程 .
.(1)求证:方程总有两个实数根;
(2)如果
 为正整数,且方程的两个根均为整数,求
为正整数,且方程的两个根均为整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为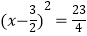
相关试题

