【题目】如图,菱形ABCD的对角线AC=12,面积为24,△ABE是等边三角形,若点P在对角线AC上移动,则PD+PE的最小值为( )

A. 4 B. 4![]() C.
C. ![]() D. 6
D. 6
参考答案:
【答案】C
【解析】
连接BD交AC于点O,连接PB,由菱形的对角线互相垂直平分可得PD=PB,得到PE+PD=PE+PB,由此可知当E、P、B共线时,PE+PD的值最小,最小值为BE的长,求出BE的长即可.
如图,连接BD交AC于O,连接PB,

∵四边形ABCD是菱形,
∴S菱形ABCD=![]() ,即
,即![]() ×12×BD=24,
×12×BD=24,
∴BD=4,
∵OA=![]() AC=6,OB=
AC=6,OB=![]() BD=2,AC⊥BD,
BD=2,AC⊥BD,
∴AB=![]() =2
=2![]() ,
,
∵AC与BD互相垂直平分,
∴PB=PD,
∴PE+PD=PE+PB,
∵PE+PB≥BE,
∴当E、P、B共线时,PE+PD的值最小,最小值为BE的长,
∵△ABE是等边三角形,
∴BE=AB=2![]() ,
,
∴PD+PE的最小值为2![]() ,
,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知反比例函数y=
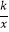 的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.
的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B. 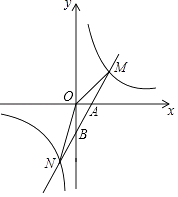
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.
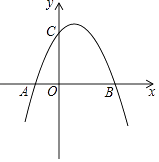
(1)求A,B,C三点的坐标?
(2)求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A,B,C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形EFGH在边长为4的正方形ABCD所在平面上移动,始终保持EF//AB,CK=1.线段KG的中点为M,DH的中点为N,则线段MN的长为 ( ).

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线y=x2+bx+c经过A、C两点.
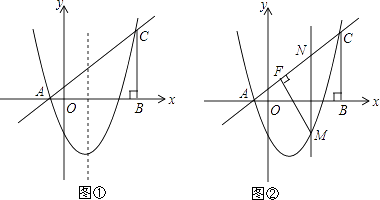
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P,Q分别向x轴作垂线,垂足为点D,E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
相关试题

