【题目】如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC 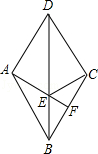
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC的什么位置?说明理由.
参考答案:
【答案】
(1)证明:连接AC.
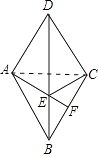
∵BD是菱形ABCD的对角线,
∴BD垂直平分AC,
∴AE=EC
(2)解:点F是线段BC的中点.
理由:∵四边形ABCD是菱形,
∴AB=CB.
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°.
∵AE=EC,
∴∠EAC= ![]() ∠CEF=30°.
∠CEF=30°.
又∵∠BAF=∠BAC﹣∠EAC=30°=∠EAC,
∴AF是等边△ABC的角平分线,
∴BF=CF,
∴点F是线段BC的中点
【解析】(1)利用菱形的对角线互相垂直平分即可证明;(2)首先证明△ABC是等边三角形,再证明AF是等边△ABC的角平分线即可;
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.

(1)说明:DC∥AB;
(2)求∠PFH的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
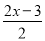 -
-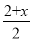 =-1; (2)解不等式组:
=-1; (2)解不等式组: 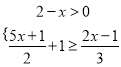
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.

(1)求∠DOF的度数;
(2)试说明OD平分∠AOG. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王计划用100元钱买乒乓球,所购买球的个数为W个,每个球的单价为n元,其中( )
A. 100是常量,W,n是变量 B. 100,W是常量,n是变量
C. 100,n是常量,W是变量 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足
 ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣9=
相关试题

