【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
参考答案:
【答案】
(1)解:∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°
(2)解:∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG
【解析】(1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解答问题:
(1)计算下列各式:
① = ,
= , 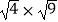 =;
=;
② = ,
= ,  = .
= .
通过计算,我们可以发现 =
=
(2)运用(1)中的结果可以得到:
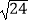 =×=
=×=
(3)通过(1)(2),完成下列问题:
①化简: ;
;
②计算: ;
;
③化简 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+5x=0的解为( )
A.x=5B.x=-5C.x1=0,x2=5D.x1=0,x2=-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A.
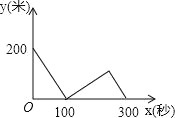 B.
B.
C.
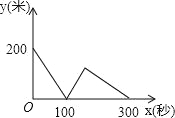 D.
D.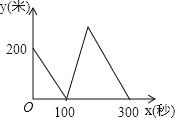
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m2﹣2n﹣1=0,则2m2﹣4n+5=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两个内角和小于第三个内角,这个三角形是( )三角形.
A. 锐角 B. 钝角 C. 直角 D. 等腰
相关试题

