【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.
参考答案:
【答案】
(1)
∵ DC∥FP,
∴∠2=∠C.
∵ ∠1=∠2,
∴∠1=∠C,
∴DC∥AB.
(2)
∵ DC∥FP,DC∥AB,
∴∠PFE=∠FED=28,∠PFG=∠AGF=80,
∴∠EFG=∠PFE+∠PFG=28+80=108,
∵ FH平分∠EFG,
∴∠EFH=![]() ∠EFG=54,
∠EFG=54,
则∠PFH=∠EFH-∠PFE=54-28=26°.
【解析】(1)根据平行线的判定定理去判断;
(2)要求∠PFH,则要求∠EFH和∠PFE,根据平行线的性质可分别求出∠EFH和∠PFE.
【考点精析】通过灵活运用角的平分线和平行线的判定,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意抛掷一枚硬币,则“正面朝上”是__事件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a﹣2)2+|b+1|=0,求:3a﹣2ab(a+b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学做数学题:已知两个多项式A,B,其中B=5x2﹣3x+6,他在求A﹣B时,把A﹣B错看成了A+B,求得的结果为8x2+2x+1.请你帮助这位同学求出A﹣B的正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图①,若BC=BD,求证:CD=DE;
(2)如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.
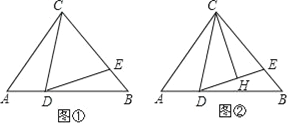
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2+2a﹣1=(a+1)2
B.a2+a2=a4
C.(﹣3ab)2=﹣9a2b2
D.a3÷a2=a -
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题不适合全面调查的是( )
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
相关试题

