【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8 ![]() ,
, ![]() ,求△DGH的面积.
,求△DGH的面积.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴AC=BC由折叠知AC=AD,BC=BD,
∴AC=AD=BC=BD,
∴四边形DBCA是菱形
(2)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,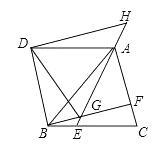
在△ABE与△BCF中,
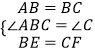 ,
,
∴△ABE≌△BCF(SAS),
∴∠AEB=∠BFC,
∵四边形DBCA是菱形,
∴DA∥BC,DB∥AC,∠BDA=∠C=60°,
∴∠HAD=∠AEB,∠DBG=∠BFC,
∴∠HAD=∠DBG,
在△DBG与△DAH中,
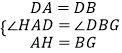 ,
,
∴△DBG≌△DAH(SAS),
∴DG=DH,∠BDG=∠ADH,
∴∠HDG=∠ADH+∠GDA=∠BDG+∠GDA=∠BDA=60°,
又∵DA=DB,DG=DH,
∴△DBA∽△DGH,
∴ ![]() ,
,
∵S△DBA= ![]() S菱形DBCA=
S菱形DBCA= ![]() ,
,
∴S△DGH= ![]()
【解析】(1)由△ABC是等边三角形和轴对称易得四边相等,证得四边形DBCA是菱形。
(2)由(1)中菱形DBCA易得△ABE≌△BCF从而利用等边三角形等量代换可得∠HAD=∠DBG,为证明△DBG≌△DAH做好条件,得到∠BDG=∠ADH最终可得△DBA∽△DGH;再利用相似三角形的面积比等于相似比的平方可得S△DGH。
【考点精析】根据题目的已知条件,利用菱形的性质和菱形的判定方法的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按A(优秀),B(良好),C(合格),D(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
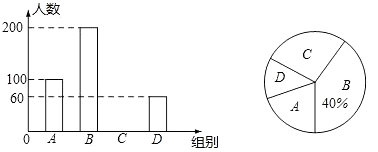
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“A”部分所对应的圆心角的度数.
(3)该市九年级共有8000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年宁波市北仑区体育中考的3个选测项目分别是50米跑,一分钟跳绳,篮球运球投篮.另规定:游泳满分的学生,只需从3个选测项目中选择一项进行测试;游泳未得满分或未参加的学生,需从3个选测项目中任选两项进行测试.
(1)小明因游泳测试获得了满分,求他在3个选测项目中选择“一分钟跳绳”项目的概率.
(2)若小红和小慧的游泳测试都未得满分,她们都必须从3个选测项目中选择两项进行体育中考测试,请用列表(或画树状图)的方法,求出小红和小慧选择的两个项目完全相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )

A.2B.4C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,推理填空:

(1)∵∠1=_______(已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=______(已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+_______=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
相关试题

