【题目】直线![]() 的解析式为
的解析式为![]() ,分别交
,分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() .
.

(1)写出![]() 两点的坐标,并画出直线
两点的坐标,并画出直线![]() 的图象.(不需列表);
的图象.(不需列表);
(2)将直线![]() 向左平移4个单位得到
向左平移4个单位得到![]() 交
交![]() 轴于点
轴于点![]() .作出
.作出![]() 的图象,
的图象,![]() 的解析式是___________.
的解析式是___________.
(3)过![]() 的顶点能否画出直线把
的顶点能否画出直线把![]() 分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线)
分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线)
参考答案:
【答案】(1)A(6,0),B(0,4);(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)分别令![]() 中
中![]() 求出与之相对应的
求出与之相对应的![]() 的值,由此即可得出点B、A的坐标,再连接AB即可;
的值,由此即可得出点B、A的坐标,再连接AB即可;
(2)根据平移的规律即可求得;
(3)可以画三条:过顶点和对边中点的直线可以把三角形面积分成相等的两部分.求出对边中点坐标,利用待定系数法即可求出函数解析式.
(1)令![]() ,
,
∴点B的坐标为(0,4);
令![]() 0,解得:
0,解得:![]() ,
,
∴点A的坐标为(6,0).
画出直线![]() 如图:
如图:
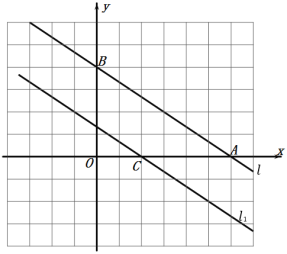
(2)将直线![]() 向左平移4个单位得到
向左平移4个单位得到![]() 1,则
1,则![]() 1的解析式为:
1的解析式为:
![]() ,
,
画出直线![]() 1如上图,
1如上图,
直线![]() 1的解析式为:
1的解析式为:![]() ;
;
(3)能画出三条,如图所示.
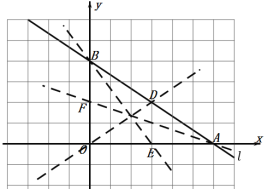
∵A(6,0),B(0,4),O(0,0),
∴AB的中点D(3,2),OA的中点E(3,0),OB的中点F(0,2);
设OD解析式为![]() ,
,
将D(3,2)代入解析式得,![]() ,
,
函数解析式为![]() ;
;
设BE解析式为![]() ,将E(3,0)代入解析式得,0=3m+4,
,将E(3,0)代入解析式得,0=3m+4,
解得![]() ,
,
函数解析式为![]() ;
;
设AF解析式为![]() ,
,
将A(6,0)代入解析式得,![]() ,
,
解得![]() ,
,
函数解析式为![]() .
.
-
科目: 来源: 题型:
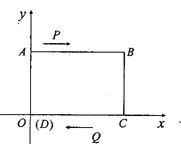
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:

⑴根据如图1,写出一个等式:
⑵如图2,若长方形的长AB为10,AD宽为6,分别求a、b的值;
⑶如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=6,ab=10,请求出阴影部分的面积.



-
科目: 来源: 题型:
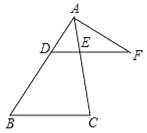
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果
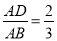 ,DE=6,求边BC的长;
,DE=6,求边BC的长;(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从
 地出发前往
地出发前往 地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达
地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达 地.下图是甲、乙两车离开
地.下图是甲、乙两车离开 地的路程
地的路程 与时间
与时间 之间的函数图象.
之间的函数图象.
(1)甲车每小时行驶_________千米,
 的值为________.
的值为________.(2)求甲车再次行驶过程中
 与
与 之间的函数关系式.
之间的函数关系式.(3)甲、乙两车离开
 地的路程差为8千米时,直接写出
地的路程差为8千米时,直接写出 的值.
的值. -
科目: 来源: 题型:
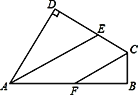
查看答案和解析>>【题目】已知:如图所示,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,AE//CF.
(1)说明:CF平分∠BCD;
(2)作△ADE的高DM,若AD=8,DE=6,AE=10,求DM的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

相关试题

