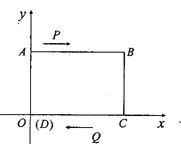
【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.
参考答案:
【答案】(1)B(8,6)(2)t为![]() (3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
(3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
【解析】
试题(1)根据点的特点可以直接写出坐标;
(2)由平行的位置和移动的距离可以设出时间t,从而构成方程解决;
(3)分在D点左右两边两种情况讨论构成的三角形,根据面积求出点的坐标.
试题解析:(1)∵AB=DC=8 AD=BC=6
∴B(8,6)
(2)运动时间为t秒 则t秒时P(3t,6)Q(8-4t,0)
∵PQ ∥BC 且 BC∥ AO
∴PQ∥A0即y轴
∴ 3t=8-4t
∴t=![]()
∴t=![]() 秒时 PQ//BC
秒时 PQ//BC
(3)∵Q在射线CD方向匀速运动.
Q在0点右侧时Q坐标(8-4t,0)
S=![]() AD.DQ
AD.DQ
∴9=![]() ×6(8-4t)
×6(8-4t)
∴t=![]()
此时8-4t=8-4×![]() =3
=3
∴Q(3,0)
Q在点0左侧时Q(8-4t,0) S=![]() AD×DQ 9=
AD×DQ 9=![]() ×6×(4t-8)
×6×(4t-8)
∴t=![]()
此时8-4t=8-4×![]() =-3
=-3
∴Q(-3,0)
∴Q点距原点3个单位时,面积为9
此时Q(3,0)或(-3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:


(1)在这次抽样调查中,一共抽取了______名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B级的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
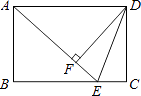
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是反比例函数y=
 的图象和一次函数y=ax+b的图象的两个交点.
的图象和一次函数y=ax+b的图象的两个交点. 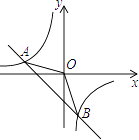
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出不等式ax+b﹣ <0的解集.
<0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每小正方形的边长为
 个单位,每个小方格的顶点叫格点.
个单位,每个小方格的顶点叫格点.
(1)画出
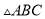 的
的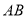 边上的中线
边上的中线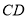 ;
;(2)画出
 向右平移
向右平移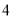 个单位后得到的
个单位后得到的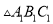 ;
;(3)图中
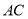 与
与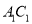 的关系是 ;
的关系是 ;(4)能使
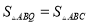 的格点
的格点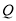 (不同于点
(不同于点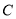 ),共有 个,在图中分别用
),共有 个,在图中分别用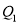 、
、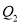 、
、 表示出来.
表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,所有房间刚好可以住满,根据经验发现,每个房间的定价每增加10元,就会有1个房间空闲,对有游客入住的房间,宾馆需对每个房间支出每天20元的各种费用.设每个房间的定价增加x元,每天的入住量为y个,客房部每天的利润为w元.
(1)求y与x的函数关系式;
(2)求w与x的函数关系式,并求客房部每天的最大利润是多少?
(3)当x为何值时,客房部每天的利润不低于14000元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC的斜边上取异于B,C的两点E,F,使∠EAF=45°,求证:以EF,BE,CF为边的三角形是直角三角形.

相关试题

