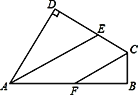
【题目】已知:如图所示,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,AE//CF.
(1)说明:CF平分∠BCD;
(2)作△ADE的高DM,若AD=8,DE=6,AE=10,求DM的长。
参考答案:
【答案】(1)略 (2)4.8
【解析】
(1)由AE∥CF,AE平分∠DAB,可证∠DAE=∠CFB,再由余角的性质可证∠DEA=∠BCF,进而可得∠DCF=∠BCF;
(2)右侧面积法求解即可.
(1)∵AE∥CF,
∴∠DEA=∠DCF,∠CFB=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠CFB,
又∵∠BCF+∠BFC=90°,∠DEA+∠DAE=90°,
∴∠DEA=∠BCF,
∴∠DEA=∠DCF=∠BCF.
∴∠DCF=∠BCF,
∴CF平分∠BCD.
(2)如图,
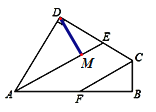
∵![]() ,
,
∴10DM=8×6,
∴DM=4.8.
-
科目: 来源: 题型:
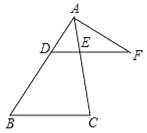
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果
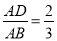 ,DE=6,求边BC的长;
,DE=6,求边BC的长;(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
 的解析式为
的解析式为 ,分别交
,分别交 轴、
轴、 轴于点
轴于点 .
.
(1)写出
 两点的坐标,并画出直线
两点的坐标,并画出直线 的图象.(不需列表);
的图象.(不需列表);(2)将直线
 向左平移4个单位得到
向左平移4个单位得到 交
交 轴于点
轴于点 .作出
.作出 的图象,
的图象, 的解析式是___________.
的解析式是___________.(3)过
 的顶点能否画出直线把
的顶点能否画出直线把 分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线)
分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从
 地出发前往
地出发前往 地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达
地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达 地.下图是甲、乙两车离开
地.下图是甲、乙两车离开 地的路程
地的路程 与时间
与时间 之间的函数图象.
之间的函数图象.
(1)甲车每小时行驶_________千米,
 的值为________.
的值为________.(2)求甲车再次行驶过程中
 与
与 之间的函数关系式.
之间的函数关系式.(3)甲、乙两车离开
 地的路程差为8千米时,直接写出
地的路程差为8千米时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).
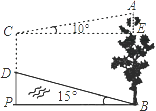
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把平面内一条数轴
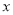 绕原点
绕原点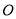 逆时针旋转角
逆时针旋转角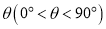 得到另一条数轴
得到另一条数轴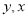 轴和
轴和 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点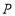 作
作 轴的平行线,交
轴的平行线,交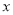 轴于点
轴于点 ,过点
,过点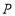 作
作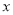 轴的平行线,交
轴的平行线,交 轴于点
轴于点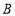 .若点
.若点 在
在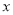 轴上对应的实数为
轴上对应的实数为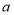 ,点
,点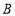 在
在 轴上对应的实数为
轴上对应的实数为 ,则成有序实数对
,则成有序实数对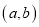 为点
为点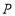 的斜坐标.
的斜坐标.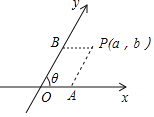
(1)在某平面斜坐标系中,已知
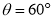 ,点
,点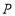 的斜坐标为
的斜坐标为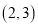 ,点
,点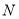 与点
与点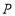 关于
关于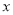 轴对称,求点
轴对称,求点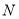 的斜坐标.
的斜坐标.(2)某平面斜坐标系中,已知点
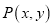 ,求出点
,求出点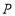 关于
关于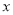 轴、
轴、 轴的对称点
轴的对称点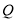 点、
点、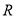 点的斜坐标.(用含
点的斜坐标.(用含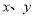 及
及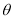 的式子表示).
的式子表示).(3)直接写出点
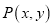 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________.
相关试题

