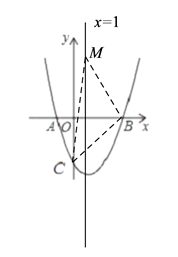
【题目】如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点,点C是抛物线与y轴的交点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)在抛物线的对称轴上是否存在点M,使△BCM是等腰三角形,若存在请直接写出点M坐标,若不存在请说明理由.
参考答案:
【答案】
(1)解:把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线顶点坐标为(1,﹣4)
(2)解:∵在y=x2﹣2x﹣3中,当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() ;抛物线顶点坐标为(1,-4),
;抛物线顶点坐标为(1,-4),
∴当0<x<3时, ![]() 的取值范围为:﹣4≤y<0
的取值范围为:﹣4≤y<0
(3)解:存在.由(1)和(2)可知,抛物线的对称轴为直线 ![]() ,点C的坐标为(0,-3),
,点C的坐标为(0,-3),
∴可设点M的坐标为(1,m),由此可得:CB2=18;CM2= ![]() ;BM2=
;BM2= ![]() .
.
①当CB2=CM2时,有 ![]() ,解得:
,解得: ![]() ;
;
②当CB2=BM2时,有 ![]() ,解得:
,解得: ![]() ;
;
③当CM2=BM2时,有 ![]() ,解得:
,解得: ![]() ;
;
综上所述,存在点M使△BCM是等腰三角形,M的坐标为: ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .
.
【解析】(1)方法一、将点A、B的坐标分别代入函数解析式,建立方程组,求出b、c的值,就可求出函数解析式;再求出顶点坐标即可。方法二、根据已知点的坐标特点,设函数解析式为交点式,即可求出函数解析式。
(2)由抛物线的开口方向和顶点坐标,可知当x=1时,y最小值=4,当x=3时,y=0;当x=0时,y=3 ,由此可求出当0<x<3时,求y的取值范围。
(3)利用函数解析式求出点C的坐标,根据已知可知点M在抛物线的对称轴上,因此设点M的坐标为(1,m),再根据点B、C的坐标,分别表示出CB2、CM2、BM2。然后分情况讨论:①当CB2=CM2时,②当CB2=BM2时,③当CM2=BM
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的AEMG的面积S1与HCFM的面积S2的大小关系是( )

A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中,且A
 、B
、B 、C
、C .将其平移后得到
.将其平移后得到 ,若A,B的对应点是
,若A,B的对应点是 ,
, ,C的对应点
,C的对应点 的坐标是
的坐标是 .
.(1)在平面直角坐标系中画出△ABC;
(2)写出点
 的坐标是_____________,
的坐标是_____________, 坐标是___________;
坐标是___________;(3)此次平移也可看作
 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
 .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积. -
科目: 来源: 题型:
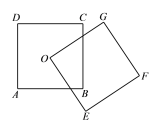
查看答案和解析>>【题目】如图所示,正方形ABCD和正方形OEFG的边长均为5,O为正方形ABCD的中心,则图中重叠部分的面积是 _______.
相关试题

