【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
参考答案:
【答案】D
【解析】
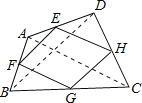
如图,根据三角形的中位线定理得到EH∥FG,EH=FG,EF=![]() BD,则可得四边形EFGH是平行四边形,若平行四边形EFGH是菱形,则可有EF=EH,由此即可得到答案.
BD,则可得四边形EFGH是平行四边形,若平行四边形EFGH是菱形,则可有EF=EH,由此即可得到答案.
如图,∵E,F,G,H分别是边AD,DC,CB,AB的中点,
∴EH=![]() AC,EH∥AC,FG=
AC,EH∥AC,FG=![]() AC,FG∥AC,EF=
AC,FG∥AC,EF=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=![]() AC,EF=
AC,EF=![]() BD,
BD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市为创建“国家园林城市”,某校举行了以“爱我冷江”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图:

根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式
 x+y+1的值.
x+y+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据x1,x2,x3,x4,x5的平均数是a,另一组数据
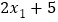 ,
,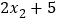 ,
,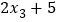 ,
,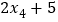 ,
,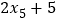 的平均数是( )
的平均数是( )A. a B. 2a C. 2a+5 D. 无法确定
-
科目: 来源: 题型:
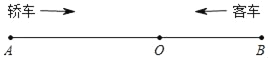
查看答案和解析>>【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
相关试题

