【题目】如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形. 
参考答案:
【答案】![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]()
【解析】解:①如图1, 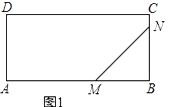
点M在AB上,点N在BC上时,t<4,BM=10﹣2t,BN=t,
∵BM=BN,
∴10﹣2t=t,
解得t= ![]() ,
,
②如图2,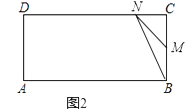
点M在BC上,点N在CD上时,5<t<7,BM=2t﹣10,CM=4﹣(2t﹣10)=14﹣2t,
CN=t﹣4,
在Rt△MCN中,MN2=(14﹣2t)2+(t﹣4)2 ,
∵BM=MN,
∴(2t﹣10)2=(14﹣2t)2+(t﹣4)2 ,
整理得,t2﹣24t+112=0,
解得t1=12﹣4 ![]() ,t2=12+4
,t2=12+4 ![]() (舍去),
(舍去),
③如图3,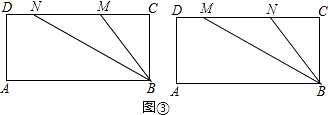
点M、N都在C、D上时,t>7,若点M在点N的右边,则CM=2t﹣14,MN=t﹣(2t﹣14)=14﹣2t,
此时BM2=(2t﹣14)2+42 ,
∵BM=MN,
∴(2t﹣14)2+42=(14﹣2t)2 , 无解,
若点M在点N的左边,则CN=t﹣4,
MN=(2t﹣14)﹣(t﹣4)=t﹣10,
此时BN2=(t﹣4)2+42 ,
∵BN=MN,
∴(t﹣4)2+42=(t﹣10)2 ,
整理得,t= ![]() (不符合题意,舍去),
(不符合题意,舍去),
④如图④,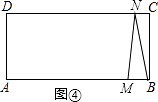
点M在AB上,点N在CD上时,BM=10﹣2t,CN=t﹣4,
由等腰三角形三线合一的性质,CN= ![]() BM,
BM,
所以,t﹣4= ![]() (10﹣2t),
(10﹣2t),
解得t= ![]() ,
,
综上所述,当运动时间为 ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() 秒时,△MBN为等腰三角形.
秒时,△MBN为等腰三角形.
故答案为: ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() .
.
分①点M在AB上,点N在BC上时,BM=BN,列出方程其解即可,②点M在BC上,点N在CD上时,表示出BM、CM、CN,再根据勾股定理列式表示出MN2 , 然后根据BM=MN列出方程其解即可;③点M、N都在C、D上时,表示出MN、CM,再根据勾股定理分两种情况列式表示出BM(或BN),然后根据BM=MN(或BN=MN)列出方程求解即可,④点M在AB上,点N在CD上时,根据等腰三角形的性质,CN= ![]() BM,然后列式求解即可.
BM,然后列式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边
长分别为m+2,m+4.(其中m为正整数)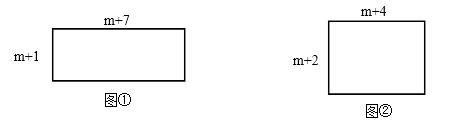
(1)图①中长方形的面积 =
=
图②中长方形的面积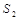 =
=
比较:
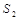 (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2)现有一正方形,其周长与图①中的长方形周长相等,则
①求正方形的边长(用含m的代数式表示);
②试探究:该正方形面积 与图①中长方形面积
与图①中长方形面积  的差(即
的差(即  -
-  )是一个常数,求出这个常数.
)是一个常数,求出这个常数.
(3)在(1)的条件下,若某个图形的面积介于 、
、 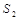 之间(不包括
之间(不包括  、
、  )并且面积为整数,这样的整数值有且只有10个,求m的值.
)并且面积为整数,这样的整数值有且只有10个,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=8cm,点P为直线MN上的点,且点P到N的距离为2cm,则线段PM=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a2b(2a﹣3b+1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
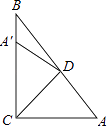
A.40°
B.30°
C.20°
D.10° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB内一点P,P1 , P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )

A.3cm
B.4cm
C.5cm
D.6cm
相关试题

