【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.

参考答案:
【答案】(1)证明见解析;(2)P(![]() ,﹣
,﹣![]() );(3)M的坐标(5,12)或(
);(3)M的坐标(5,12)或(![]() ,﹣
,﹣![]() )
)
【解析】试题分析:(1)先利用待定系数法求二次函数的解析式,并配方成顶点式求顶点D的坐标,和与y轴的交点C的坐标,由勾股定理计算△BDC三边的平方,利用勾股定理的逆定理证明△BCD是直角三角形;
(2)作辅助线,构建直角三角形PCQ与直角三角形BDC相似,根据比例式表示出点P的坐标,利用待定系数法求直线BD的解析式,因为点P为线段BD上一点,代入直线BD的解析式列方程可求出点P的坐标;
(3)同理求直线CD的解析式为:y=-x-3,由此表示点N的坐标为(a,-a-3),因为M在抛物线上,所以设M(x,x2-2x-3),根据同角的三角函数得:tan∠BDE=tan∠CMN=![]() ,则
,则 ![]() ,如图2,证明△MGN∽△NFC,列比例式可得方程组解出即可;如图3,证明△CFN∽△NGM,列比例式可得方程组解出即可;
,如图2,证明△MGN∽△NFC,列比例式可得方程组解出即可;如图3,证明△CFN∽△NGM,列比例式可得方程组解出即可;
试题解析:
解:(1)把A(﹣1,0)和B(3,0)两点代入抛物线y=x2+bx+c中得:
![]() , 解得:
, 解得: ![]() ,
,
∴抛物线的解析式为:y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴C(0,﹣3),D(1,﹣4),
由勾股定理得:BC2=32+32=18,
CD2=12+(4﹣3)2=2, BD2=(3﹣1)2+42=20,
∴CD2+BC2=BD2, 即∠BCD=90°,
∴△BCD是直角三角形;
(2)作PQ⊥OC于点Q,

∴∠PQC=90°,
∵∠PCO+∠CDB=180°,
∠PCO+∠PCQ=180°,
∴∠CDB=∠PCQ,
∵∠PQC=∠BCD=90°,
∴△PCQ∽△BDC,
∴![]() =3,
=3,
∴PQ=3CQ,
设CQ=m,则PQ=3m,
设P(3m,﹣3﹣m),
设直线BD的解析式为:y=kx+b,
把B(3,0)、D(1,﹣4)代入得: ![]() ,解得:
,解得: ![]() ,
,
∴直线BD的解析式为:y=2x﹣6,
将点P的坐标代入直线BD:y=2x﹣6得:
﹣3﹣m=2×3m﹣6,
∴3m=![]() ,﹣3﹣
,﹣3﹣![]() =﹣
=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() );
);
(3) M的坐标(5,12)或(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠A的余角是20°,那么∠A等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边
长分别为m+2,m+4.(其中m为正整数)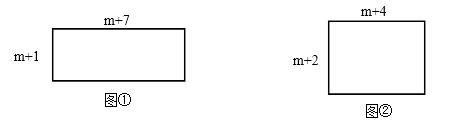
(1)图①中长方形的面积 =
=
图②中长方形的面积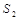 =
=
比较:
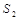 (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2)现有一正方形,其周长与图①中的长方形周长相等,则
①求正方形的边长(用含m的代数式表示);
②试探究:该正方形面积 与图①中长方形面积
与图①中长方形面积  的差(即
的差(即  -
-  )是一个常数,求出这个常数.
)是一个常数,求出这个常数.
(3)在(1)的条件下,若某个图形的面积介于 、
、 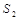 之间(不包括
之间(不包括  、
、  )并且面积为整数,这样的整数值有且只有10个,求m的值.
)并且面积为整数,这样的整数值有且只有10个,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=8cm,点P为直线MN上的点,且点P到N的距离为2cm,则线段PM=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a2b(2a﹣3b+1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
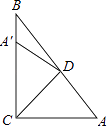
A.40°
B.30°
C.20°
D.10°
相关试题

