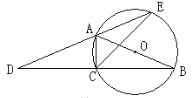
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB= ![]() ,BC-AC=2,求CE的长。
,BC-AC=2,求CE的长。
参考答案:
【答案】(1)、证明过程见解析;(2)、4.
【解析】
试题分析:(1)、根据直径可得∠ACB=90°,根据DC=CB得出AD=AB,从而得出答案;(2)、设BC=x,则AC=x-2,根据△ABC的勾股定理求出x的值,从而得出CE的长度.
试题解析:(1)、∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,
又∵DC=CB,∴AD=AB,∴∠B=∠D;
(2)、设BC=x,则AC=x-2,
在Rt△ABC中,AC2+BC2=AB2,∴(x-2)2+x2=(![]() )2,
)2,
解得x=4或-2(舍去)即BC=4
又∵⊙O中,∠E=∠B,∴∠D=∠E ∴CE=CD=BC=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程
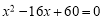 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积. 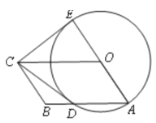
-
科目: 来源: 题型:
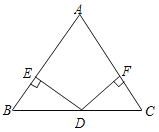
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α、β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A.α=β;
B.α+β=90°;
C.α-β=90°;
D.β-α=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A是锐角,那么△ABC是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数组2,2,x,3,4的平均数为3,则这组数中的( )
A. x=3B. 中位数为3C. 众数为3D. 中位数为x
-
科目: 来源: 题型:
查看答案和解析>>【题目】秋收起义广场是为纪念秋收起义而建设的纪念性广场,位于萍乡城北新区,占地面积约为109000平方米,将数据109000用科学记数法表示为 .
相关试题

