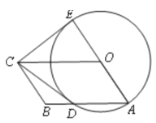
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程![]() 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
参考答案:
【答案】(1)、证明过程见解析;(2)、48.
【解析】
试题分析:(1)、连接OD,根据切线得出∠OEC=90°,根据OD=OA以及OC∥AD得出∠OAD=∠EOC,则∠EOC=∠DOC,结合OD=OE,OC=OC得出△ODC和△OEC全等,从而得出∠ODC=∠OEC=90°,得出切线;(2)、根据方程得出OC=10,OA=6,根据勾股定理得出CD=8,根据全等得出CE=8,然后计算四边形的面积.
试题解析:(1)、连OD,∵CE是⊙O的切线, ∠OEC=90O ,∵OD=OA,∴∠ODA=∠OAD,又∵OC//AD
∴∠OAD =∠EOC,∠DOC=∠ODA,∴∠EOC=∠DOC, 又∵OD=OE,OC=OC, ∴△ODC≌△OEC(SAS)
∴∠ODC=∠OEC=90 O, ∴CD是⊙O的切线。
(2)、![]() ,
,![]() ,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
∴平行四边形OABC的面积S=OA×CE=6×8=48
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.m2m3=m6B.(m2)3=m5C.m3÷m2=mD.3m﹣m=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的平方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有理数m,n满足|m|=8,|n|=5,mn<0,求m﹣n的值.
-
科目: 来源: 题型:
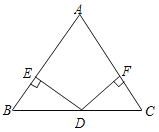
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α、β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A.α=β;
B.α+β=90°;
C.α-β=90°;
D.β-α=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB=
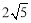 ,BC-AC=2,求CE的长。
,BC-AC=2,求CE的长。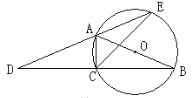
相关试题

