【题目】如图Ⅰ,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3.
(1)如图Ⅱ,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,设BC=a,AC=b,AB=c,请你确定S1、S2、S3之间的关系并证明.
(2)如图Ⅲ,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系.(不必证明)
(3)若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?(不必证明)

参考答案:
【答案】(1)(1)S1=S2+S3,证明见解析;
(2)S1=S2+S3;
(3)S1=S2+S3
【解析】试题分析:(1)从图1的规律可得S1=S2+S3;
(2)根据勾股定理求得等边三角形的高,再求出面积,可得S1=S2+S3;
(3)根据两相似三角形的面积比等于相似比的平方,可得![]() ,
, ![]() ,∴
,∴![]() ,∴S1=S2+S3.
,∴S1=S2+S3.
试题解析:(1)设Rt△ABC三边BC,CA,AB的长分别为a,b,c,则c2=a2+b2.
∴S1=S2+S3
(2)S1=S2+S3,证明如下:
显然S1=![]() c2,S2=
c2,S2=![]() a2,S3=
a2,S3=![]() b2,
b2,
∴S2+S3=![]() (a2+b2)=
(a2+b2)=![]() c2=S1.
c2=S1.
(3)当所作的三个三角形相似时,S1=S2+S3.
∵所作三个三角形相似.
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴S1=S2+S3.
即凡是向△ABC外做相似多边形,S1=S2+S3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1.17-32-23中把省略的“+”号填上应得到( )
A. 1.17+32+23
B. -1.17+(-32)+(-23)
C. 1.17+(-32)+(-23)
D. 1.17-(+32)-(+23)
-
科目: 来源: 题型:
查看答案和解析>>【题目】地图上某地的面积为100cm2,比例尺是l:500,则某地的实际面积是_______m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若整式xn﹣2﹣5x+2是关于x的三次三项式,那么n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店第一次用500元购进某种水果,由于销售状况良好,该店又用1650元购时该品种水果,所购数量是第一次购进数量的3倍,但进货价每千克多了0.5元.
(1)第一次所购水果的进货价是每千克多少元?
(2)水果店以每千克8元销售这些水果,在销售中,第一次购进的水果有5%的损耗,第二次购进的水果有2%的损耗.该水果店售完这些水果可获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
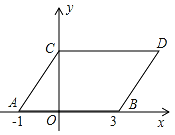
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2 .
相关试题

