Question

【题目】如图1，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|a+2|+（b﹣4）2=0.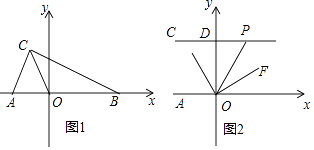

（1）求a，b的值．
（2）在坐标轴上是否存在一点M，使△COM的面积= △ABC的面积，求出点M的坐标．
（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上的一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时， 的值是否会改变？若不变，求其值；若改变，说明理由．

Answer 1

【答案】
（1）

解：∵|a+2|+（b﹣4）2=0，

|a+2|≥0，（b﹣4）2≥0，

∴a=﹣2，b=4．

（2）

解：由（1）可知A（﹣2，0），B（4，0），

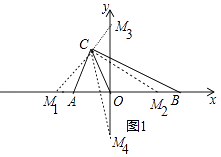
①当M在x轴上时，设M（m，0），

由题意： |m|2= 62，

∴m=±3，

∴M（3，0）或（﹣3，0）．

②当M在y轴上时，设M（0，m），

由题意： |m|1= 62，

∴m=±6，

∴M（6，0）或（0，﹣6），

综上所述，满足条件的点M坐标为（3，0）或（﹣3，0）或（0，6）或（0，﹣6）．

（3）

解：如图2中，结论： 的值是定值， =2．

理由：∵OE⊥OF，

∴∠EOF=90°，

∴∠AOE+∠FOG=90°，

∵∠AOE=∠EOP，∠EOP+∠POF=90°，

∴∠FOG=∠POF，

∵∠DOE+∠AOE=90°，∠AOE+∠FOG=90°，

∴∠DOE=∠FOG，

∵CP∥AG，

∴∠OPD=∠POG=2∠FOG，

∴∠OPD=2∠FOG，

∴ =2．

【解析】（1）根据非负数的性质即可解决问题．（2）分两种情形讨论①当M在x轴上时，设M（m，0），由题意： |m|2= 62．②当M在y轴上时，设M（0，m），由题意： |m|1= 62，解方程即可解决问题．（3）结论： 的值是定值．只要证明∠DOE=∠FOG，∠OPD=2∠FOG即可．
【考点精析】关于本题考查的三角形的“三线”和三角形三边关系，需要了解1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内；三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边才能得出正确答案．