【题目】关于x的方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根。
(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=![]() +
+![]() + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
参考答案:
【答案】(1)详见解析;(2)S的值能为2,此时k的值为2.
【解析】
试题分析:(1) 本题二次项系数为(k-1),可能为0,可能不为0,故要分情况讨论;要保证一元二次方程总有实数根,就必须使△>0恒成立;(2)欲求k的值,先把此代数式变形为两根之积或两根之和的形式,代入数值计算即可.
试题解析:⑴①当k-1=0即k=1时,方程为一元一次方程2x=1,
x=![]() 有一个解;
有一个解;
②当k-1≠0即k≠1时,方程为一元二次方程,
△=(2k)-4×2(k-1)=4k-8k+8=4(k-1) +4>0
方程有两不等根
综合①②得不论k为何值,方程总有实根
⑵∵x +x =![]() ,x x =
,x x =![]()
∴S=![]() +
+![]() + x1+x2
+ x1+x2
=![]()
=![]()
=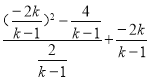
=![]()
=2k-2=2,
解得k=2,
∴当k=2时,S的值为2
∴S的值能为2,此时k的值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+(b﹣4)2=0.
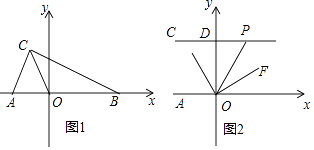
(1)求a,b的值.
(2)在坐标轴上是否存在一点M,使△COM的面积= △ABC的面积,求出点M的坐标.
△ABC的面积,求出点M的坐标.
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,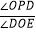 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法把代数式3x-2x2-2化为a(x+m)2+n的形式,并说明不论x取何值,这个代数式的值总是负数.并求出当x取何值时,这个代数式的值最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2﹣3与y轴的交点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A.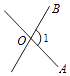
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC~△DEF,相似比为9:4,则△ABC与△DEF对应中线的比为( )
A.9:4B.4:9C.81:16D.3:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不能判定一个四边形是平行四边形的是( )
A. 两组对边分别平行的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行另一组对边相等的四边形是平行四边形
D. 对角线互相平分的四边形是平行四边形
相关试题

