【题目】已知 A(0,a),B(b,0),a、b 满足.a+b=4,a-b= 12,
(1)求 a、b 的值;
(2)在坐标轴上找一点 D,使三角形 ABD 的面积等于三角形 OAB 面积的一半, 求 D 点坐标;
(3)作∠BAO 平分线与∠ABC 平分线 BE 的反向延长线交于 P 点,求∠P 的度数.

参考答案:
【答案】(1)a=8,b=-4;(2)D(-2,0) 或(-8,0)或(0,4) 或(0,16);(3)45°.
【解析】
(1)根据已知列方程组即可求出a、b的值
(2)分点D在x轴上和y轴上进行解答即可
(3)根据三角形的一个外角等于与它不相邻的两个内角的和,列式求出∠ABC,再根据角平分线的定义求出∠ABE和∠BAP,然后根据三角形的一个外角等于与它不相邻的两个内角的和,列式计算即可得解.
解:(1)∵a+b=4,a-b= 12,
∴a=8,b=-4
(2)当点D在x轴上时,
∵三角形 ABD 的面积等于三角形 OAB 面积的一半,
∴D为OB的中点或BD=OB,∴D(-2,0)或(-8,0)
当点D在y轴上时,
∵三角形 ABD 的面积等于三角形 OAB 面积的一半,
∴D为OA的中点或OA=AD,∴D(0,4)或(0,16)
∴D(-2,0) 或(-8,0)或(0,4) 或(0,16)
(3)根据三角形的外角性质,可得∠ABC=∠AOB+∠BAO,
∵BE平分∠CBA,AP平分∠BAO,
∴∠ABE=![]() ∠ABC,∠BAP=
∠ABC,∠BAP=![]() ∠BAO,
∠BAO,
∴∠P=∠ABE-∠BAP=![]() (∠AOB+∠BAO)-
(∠AOB+∠BAO)-![]() ∠BAO=
∠BAO=![]() ∠AOB,
∠AOB,
∵∠AOB=90°,
∴∠P=![]() ×90°=45°.
×90°=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
-
科目: 来源: 题型:
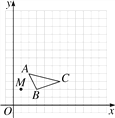
查看答案和解析>>【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点E、F是BC、CD的中点,且AE⊥BC,AF⊥CD.

(1)求证:AB=AD.
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
-
科目: 来源: 题型:
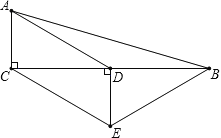
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE//AD,若AC=2,CE=4,则四边形ACEB的周长为 ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
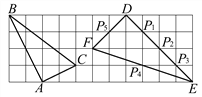
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

相关试题

