搜索
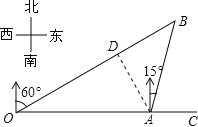
【题目】如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，求该船航行的距离（即AB的长）．
参考答案：
【答案】
【解析】试题分析：过点A作AD⊥OB于D．先解Rt△AOD，得出AD=
OA=2km，再由△ABD是等腰直角三角形，得出BD=AD=2km，则AB=
AD=
km．
解：如图，过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°，OA=4km，
∴AD=
OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB∠AOB=75°30°=45°
∴BD=AD=2km，
∴AB=
AD=
km.
即该船航行的距离(即AB的长)为
kkm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知 A(0，a)，B(b，0)，a、b 满足.a+b=4，a-b= 12，
（1）求 a、b 的值；
（2）在坐标轴上找一点 D，使三角形 ABD 的面积等于三角形 OAB 面积的一半， 求 D 点坐标；
（3）作∠BAO 平分线与∠ABC 平分线 BE 的反向延长线交于 P 点，求∠P 的度数.
-
科目： 来源： 题型：
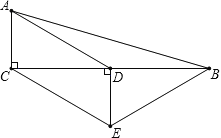
查看答案和解析>>【题目】如图，在△ABC中，∠ACB＝90°，D是BC的中点，DE⊥BC，CE//AD，若AC＝2，CE＝4，则四边形ACEB的周长为 ▲ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1、P2、P3、P4、P5是△DEF边上的5个格点，请按要求完成下列各题：
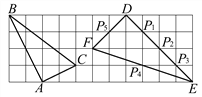
(1)试证明△ABC为直角三角形；
(2)判断△ABC和△DEF是否相似，并说明理由；
(3)直接写出一个与△ABC相似的三角形，使它的三个顶点为P1、P2、P3、P4、P5中的三个格点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC关于点C成中心对称的△A1B1C1．
（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2．
（3）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，A、B两点的坐标分别为A(0，m)、B(n，0)，且|m﹣n﹣3|+
＝0，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P的运动时间为t秒．(1)求OA、OB的长；
(2)连接PB，设△POB的面积为S，用t的式子表示S；
(3)过点P作直线AB的垂线，垂足为D，直线PD与x轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB？若存在，请求出t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
相关试题
