【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.

参考答案:
【答案】(1)C(0,2),D(4,2),8;(2)Q点的坐标为(0,4)或(0,-4);(3)见解析
【解析】试题分析:(1)依题意知,将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,故C、D两点点y值为2. 所以点C,D的坐标分别为C(0,2),D(4,2) ,
四边形ABDC的面积S四边形ABDC=CO×AB=2×4=8
(2)(2)在y轴上是否存在一点P,使S△PAB=S四边形ABDC.理由如下:
设点P到AB的距离为h,
S△PAB=![]() ×AB×h=2h,
×AB×h=2h,
由S△PAB=S四边形ABDC,得2h=8,
解得h=4,
∴P(0,4)或(0,-4).
(3)①是正确的结论,过点P作PQ∥CD,
因为AB∥CD,所以PQ∥AB∥CD(平行公理的推论)
∴∠DCP=∠CPQ,∵∠BOP=∠OPQ(两直线平行,内错角相等),
∴∠DCP+∠BOP=∠CPQ +∠OPQ =∠CPO
所以![]() =
=![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣3(x﹣1)2+2的开口向_____,对称轴为_____,顶点坐标为_____.
-
科目: 来源: 题型:
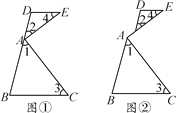
查看答案和解析>>【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c、d是成比例线段,其中a=5,b=2.5,c=8,则线段d的长为( )
A.2B.4C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若xm+1+1+2(m﹣1)x+1=0是关于x的一元二次方程,则m的值是( )
A.﹣1B.0C.1D.2
-
科目: 来源: 题型:
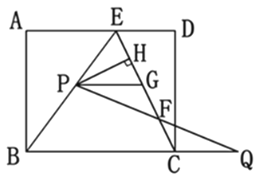
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
(3)作PH⊥EC于点H.探究:
①点P在运动过程中,线段HF的长度是否发生变化?若变化,说明理由;若不变,求HF的长度;
②当x为何值时,△PHF与△BAE相似
相关试题

