Question

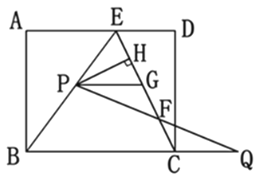
【题目】如图，在矩形ABCD中，E是AD上一点，AB=8，BE=BC=10，动点P在线段BE上（与点B、E不重合），点Q在BC的延长线上，PE=CQ，PQ交EC于点F，PG∥BQ交EC于点G，设PE=x.

（1）求证：△PFG≌△QFC

（2）连结DG.当x为何值时，四边形PGDE是菱形，请说明理由；

（3）作PH⊥EC于点H.探究：

①点P在运动过程中，线段HF的长度是否发生变化？若变化，说明理由；若不变，求HF的长度；

②当x为何值时，△PHF与△BAE相似

Answer 1

【答案】（1）证明见解析；（2）当x=4时，四边形PGDE是菱形，理由见解析；（3）①不变化，HF，②当或时，△PHF与△BAE相似

【解析】试题分析:(1)根据全等三角形的判定ASA即可证出;(2)先证出PG∥BQ，AD∥BC得到四边形PGDE是平行四边形，再根据四边形PGDE是菱形得出PG=PE=4；（3）① 证出△PFG≌△QFC，求出HF的长；②分两种情况讨论得出.

试题解析:

(1)证明：∵BC=BE ∴∠BCE=∠PEC

∵PG∥BQ

∴∠BCE=∠PGE, ∠Q=∠FPG ，∠QCF=∠PGF

∴∠PGE=∠PEC

∴PE=PG

∵PE=CQ

∴ PG =CQ

∴△PFG≌△QFC （ASA）

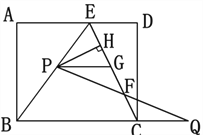
（2）连结DG.当x=4时，四边形PGDE是菱形，

理由如下；

∵四边形ABCD是矩形，

∴AD∥BC

AB=CD=8，AD=BC=BE=10

在Rt△ABE中

AE=

∴DE=AD-AE=10-6=4

由（1）知PG=PE=x=4

∴PG=DE

∵PG∥BQ，AD∥BC

∴PG∥DE

∴四边形PGDE是平行四边形，

∵PG=PE=4

∴四边形PGDE是菱形

（3）①不变化

在Rt△ABE中

CE=

∵PG=PE，PH⊥EC

∴EH=HG=EG（等腰三角形“三线合一”）

∵△PFG≌△QFC

∴CF=GF=CG

∴HF=HG+FG=EG+CG=CE=

②∵PG∥DE, ∴∠DEC=∠PGH

在Rt△PGH中

PH=PG×sin∠PGH= x×sin∠DEC= x×= x×=

分两种情况讨论：

（I）若△PHF/span>∽△EAB，则

∴

∴

∴当时，△PHF∽△BAE.

（II）若△PHF∽△BAE，则

∴

∴

∴当或时，△PHF与△BAE相似