Question

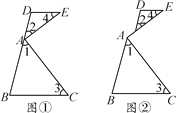
【题目】如图，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.

(1)如图①，求证：DE∥BC；

(2)若将图①改变为图②，其他条件不变，(1)中的结论是否仍成立？请说明理由．

Answer 1

【答案】见解析

【解析】（1）首先证明∠1+∠3+∠2+∠4=180°，进而证明∠D+∠B=180°，即可解决问题．
（2）如图，作辅助线，证明∠AEC+∠ACE+∠3+∠4=180°，即可解决问题．

试题解析：（1）如图1，

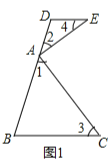
∵∠1=∠3，∠2=∠4，

∴∠1+∠3+∠2+∠4=2（∠1+∠2），

∵∠1+∠2=90°，

∴∠1+∠3+∠2+∠4=180°；

∵∠D+∠B+∠1+∠3+∠2+∠4=360°，

∴∠D+∠B=180°，

∴DE∥BC．

（2）成立．

如图2，连接EC；

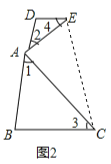
∵∠1=∠3，∠2=∠4，且∠1+∠2=90°，

∴∠3+∠4=∠1+∠2=90°；

∵∠EAC=90°，

∴∠AEC+∠ACE=180°-90°=90°，

∴∠AEC+∠ACE+∠3+∠4=180°，

∴DE∥BC，

即（1）中的结论仍成立．