【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处. 
(1)若∠PEF=48°,点F恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
参考答案:
【答案】
(1)解:①如图1,
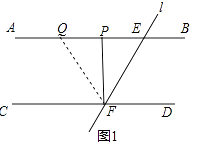
当点Q落在AB上,
∴FP⊥AB,
∴∠EFP=90°﹣∠PEF=42°,
②如图2,
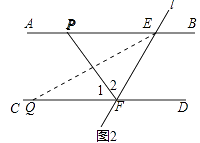
当点Q落在CD上,
∵将△EPF沿PF折叠,使顶点E落在点Q处,
∴PF垂直平分EQ,
∴∠1=∠2,
∵AB∥CD,
∴∠QFE=180°﹣∠PEF=132°,
∴∠PFE= ![]() QFE=66°
QFE=66°
(2)解:①如图3,

当点Q在平行线AB,CD之间时,
设∠PFQ=x,由折叠可得∠EFP=x,
∵∠CFQ= ![]() PFC,
PFC,
∴∠PFQ=∠CFQ=x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴75°+x+x+x=180°,
∴x=35°,
∴∠EFP=35°;
②如图4,

当点Q在CD的下方时,
设∠CFQ=x,由∠CFQ= ![]() PFC得,∠PFC=2x,
PFC得,∠PFC=2x,
∴∠PFQ=3x,
由折叠得,∠PFE=∠PFQ=3x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2x+3x+75°=180°,
∴x=21°,
∠EFP=3x=63°,
综上所述,∠EFP的度数是35°或63°
【解析】(1)①如图1,当点Q落在AB上,根据三角形的内角和即可得到结论;①如图2,当点Q落在CD上,由折叠的性质得到PF垂直平分EQ,得到∠1=∠2,根据平行线的性质即可得到结论;(2)①如图3,当点Q在平行线AB,CD之间时,设∠PFQ=x,由折叠可得∠EFP=x根据平行线的性质即可得到结论;②如图4,当点Q在CD的下方时,设∠CFQ=x,由∠CFQ= ![]() PFC得,∠PFC=2x根据平行线的性质即可得到结论.
PFC得,∠PFC=2x根据平行线的性质即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).

A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人的眼睛可以看见的红光的波长为0.000077cm,用科学记数法精确到0.00001cm表示为____cm.
-
科目: 来源: 题型:
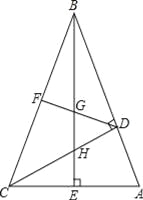
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作:
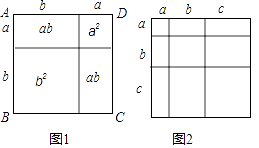
(i)把它看成是一个大正方形,则它的面积为(a+b)2;
(ii)把它看成是2个小长方形和2个小正方形组成的,则它的面积为a2+2ab+b2;因此,可得到等式:(a+b)2=a2+2ab+b2 .
(1)类比教材中的方法,由图2中的大正方形可得等式: .
(2)试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图(标注好a,b) ,由图形可知,多项式2a2+3ab+b2可分解因式为: .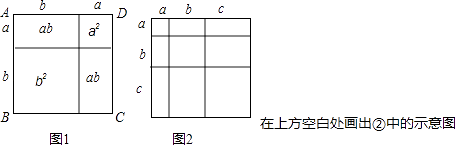
(3)若将代数式(a1+a2+a3+…+a20)2展开后合并同类项,得到多项式N,则多项式N的项数一共有项. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(5,y1)和B(2,y2)都在直线y=﹣x上,则y1与y2的关系是( )
A.y1≥y2
B.y1=y2
C.y1<y2
D.y1>y2
相关试题

