【题目】点A(5,y1)和B(2,y2)都在直线y=﹣x上,则y1与y2的关系是( )
A.y1≥y2
B.y1=y2
C.y1<y2
D.y1>y2
参考答案:
【答案】C
【解析】解:∵点A(5,y1)和B(2,y2)都在直线y=﹣x上,
∴y1=﹣5,y2=﹣2,
∵﹣5<﹣2,
∴y1<y2 .
故选:C.
分别把点A(5,y1)和B(2,y2)代入直线y=﹣x,求出y1 , y2的值,再比较出其大小即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.

(1)若∠PEF=48°,点F恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
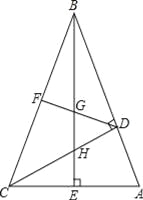
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作:
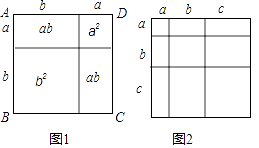
(i)把它看成是一个大正方形,则它的面积为(a+b)2;
(ii)把它看成是2个小长方形和2个小正方形组成的,则它的面积为a2+2ab+b2;因此,可得到等式:(a+b)2=a2+2ab+b2 .
(1)类比教材中的方法,由图2中的大正方形可得等式: .
(2)试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图(标注好a,b) ,由图形可知,多项式2a2+3ab+b2可分解因式为: .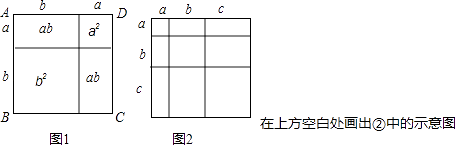
(3)若将代数式(a1+a2+a3+…+a20)2展开后合并同类项,得到多项式N,则多项式N的项数一共有项. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A. 掷一次骰子,向上一面的点数是6
B. 任意画个三角形,其内角和为180°
C. 篮球队员在罚球线上投篮一次,未投中
D. 一元二次方程一定有两个实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某种商品,成本为30元/件,当销售价格为60元件/时,每天可售出100件,经市场调查发现,销售单价每降1元,每天销量增加10件.当销售单价为__________元时,每天获取的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润.
相关试题

