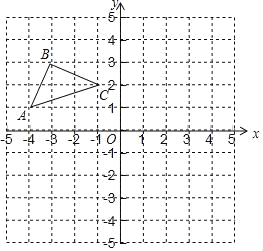
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标:A1( ),B1( ),C1( );
(2)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,连接C1C2,CC2,C1C,并直接写出△CC1C2的面积是 .
参考答案:
【答案】(1)画图见解析;(﹣4,﹣1),(﹣3,﹣3),(﹣1,﹣2);(2)坐标见解析;![]() =6.
=6.
【解析】
(1)分别作出A、B、C关于x轴对称点A1、B1、C1即可解答;(2)分别作出A、B、C的对应点A2、B2、C2即可解答,结合图形,利用三角形的面积公式即可求得△CC1C2的面积.
(1)△A1B1C1如图所示,:A1(﹣4,﹣1),B1(﹣3,﹣3),C1(﹣1,﹣2);
故答案为(﹣4,﹣1),(﹣3,﹣3),(﹣1,﹣2);

(2)△A2B2C2如图所示,![]() =
=![]() ×4×3=6.
×4×3=6.
故答案为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:

①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
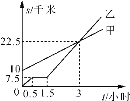
查看答案和解析>>【题目】如图,分别表示甲步行与乙骑自行车(在同一路上)行走的路程s甲,s乙与时间t的关系,观察图象并回答下列问题:
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙的自行车发生故障,停下来修车的时间为 小时;
(3)乙从出发起,经过 小时与甲相遇;
(4)乙骑自行车出故障前的速度与修车后的速度一样吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,淇淇的爸爸去参加一个聚会,淇淇坐在汽车上用所学知识绘制了一张反映汽车速度与时间的关系图,第二天,淇淇拿着这张图给同学看,并向同学提出如下问题,你能回答吗?
(1)在上述变化过程中,自变量是什么?因变量是什么?
(2)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(3)汽车在哪段时间保持匀速行驶?速度是多少?
(4)用语言大致描述这辆汽车的行驶情况.

-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC,不是直角三角形的是( )
A. b2=a2﹣c2 B. a:b:c=3:4:5
C. ∠C=∠A﹣∠B D. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由


相关试题

