【题目】如图,网格中有格点△ABC与△DEF.

(1)△ABC与△DEF是否全等?(不说理由.)
(2)△ABC与△DEF是否成轴对称?(不说理由.)
(3)若△ABC与△DEF成轴对称,请画出它的对称轴l.并在直线l上画出点P,使PA+PC最小.
参考答案:
【答案】(1)△ABC△DEF;(2)△ABC与△DEF成轴对称;(3)见详解
【解析】
(1)根据坐标系可以看出△ABC与△DEF三边相等,即可证明△ABC与△DEF全等;(2)根据坐标系可以看出△ABC与△DEF关于某条直线对称;(3)利用网格特点,作AD的垂直平分线即可得出对称轴l,连接CD,与直线l的交点即为所求;
解:(1)根据坐标系可以看出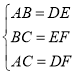
∴△ABC△DEF;
(2)根据坐标系可以看出△ABC与△DEF关于直线l成轴对称;
(3)要使PA+PC最小则A,P,C三点共线的时候即为所求因为点D为A的对称点,所以连接PD与对称轴交点即为所求,如图所示
点P即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=
 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

-
科目: 来源: 题型:
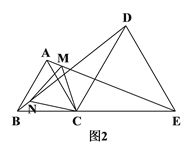
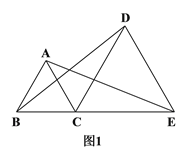
查看答案和解析>>【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
相关试题

