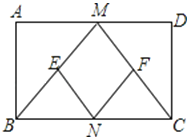
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)四边形MENF是菱形;理由见解析.
【解析】(1)由矩形的性质得出AB=DC,∠A=∠D,再由M是AD的中点,根据SAS即可证明△ABM≌△DCM;
(2)先由(1)得出BM=CM,再由已知条件证出ME=MF,EN、FN是△BCM的中位线,即可证出EN=FN=ME=MF,得出四边形MENF是菱形.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中,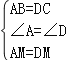 ,
,
∴△ABM≌△DCM(SAS);
(2)解:四边形MENF是菱形;理由如下:
由(1)得:△ABM≌△DCM,
∴BM=CM,
∵E、F分别是线段BM、CM的中点,
∴ME=BE=![]() BM,MF=CF=
BM,MF=CF=![]() CM,
CM,
∴ME=MF,
又∵N是BC的中点,
∴EN、FN是△BCM的中位线,
∴EN=![]() CM,FN=
CM,FN=![]() BM,
BM,
∴EN=FN=ME=MF,
∴四边形MENF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
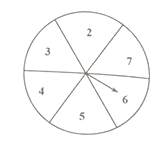
求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在x轴上,坐标为(0,3),点B在x轴上.
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=
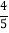 ,求点M的坐标.
,求点M的坐标.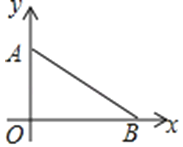
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=
 .
.(1)求旗杆EF的高;
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
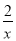 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.(1)求一次函数的解析式;
(2)对于反比例函数y=
 ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.
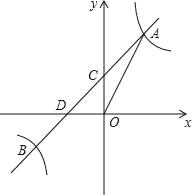
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形连接AC交EF于G,下列结论: ①BE=DF,②∠DAF=15°,③AC⊥EF,④BE+DF=EF,⑤EC=FG;其中正确结论有( )个

A.2B.3C.4D.5
相关试题

